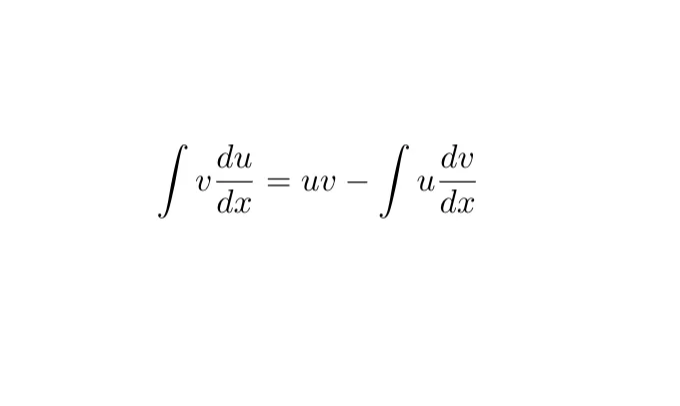
최근에 나는 스스로에게 물었습니다: 만약 나가 수학 고등학교 선생님이라면, 어떻게 내 가장 밝은 학생들을 독려하고 그들이 훌륭한 수학자가 될 수 있도록 준비할까?
고등학교에서 수학을 공부했던 시절을 생각해보니, 많은 수학 교육과정이 학생들에게 매우 메모리적이고 공식적인 방식으로 전해진다는 것을 깨달았습니다. 학생들에게 주어진 문제 유형에 대한 기본 접근 방식과 공식이 제시되며, 그들은 이를 효과적으로 활용할 수 있도록 시험지에서 문제가 발생할 때까지 반복적으로 접근 방식을 연습합니다.
그러나 공식적 문제에 접근하는 방법을 배운다고 해서 반드시 가르치는 개념의 의미를 완전히 이해하고 감사할 수 있는 것은 아닙니다. 그리고 가르쳐지는 개념의 의미를 완전히 이해하지 못한다면, 그 개념들을 생소한 영역에서 어떻게 적용해야 하는 지 알지 못할 것입니다.
따라서 수학자가 되기 위해, 지혜로운 목표를 상급 레벨로 끌어올려야 할 때 도전해야 합니다. 이러한 상황에서 공식은 실제로 무엇을 나타내는지 제대로 이해하지 못할 때 도움이 되지 않습니다. 그래서 일반적인 고등학교 수학 주제를 가르치는 방법에 대해 생각해볼 때 공식을 넘어서 학생들이 공식이 나타내는 것을 이해하도록 도와줄 수 있는 방법이 무엇인지 고민하게 되었습니다.
부분 적분
고등학교 수학에서 가르치는 매우 흔한 방법 중 하나인 부분 적분입니다. 부분 적분은 함수들의 곱을 적분하는 데 사용되는 공식입니다. 함수 v(x)와 다른 함수 u(x)의 도함수 du/dx가 주어졌을 때, 이 공식을 사용하여 그들의 곱의 적분을 계산하는 데 도움을 줄 수 있습니다:
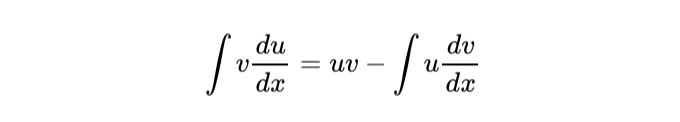
간단한 예는 y = xcosx의 적분을 계산하는 것입니다. 만약 v = x이고 du/dx = cosx이면, 우리의 공식에 따르면:
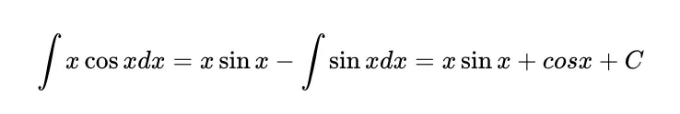
여기서 C는 우리의 표준적 적분 상수입니다.
물론, 적분부분법의 일반 공식은 도함수의 곱셈 법칙에서 직접 유도됩니다만, 나는 그 공식을 외우는 것 외에 다른 방법으로 이해하려고 노력해 보지 않았습니다. 이 기사에서는 적분부분법의 공식에 대한 몇 가지 멋진하고 유용한 기하학적 해석을 개발할 수 있다는 것을 보여주고 싶습니다. 이것이 개념에 대한 더 깊은 이해를 돕는다고 생각합니다. 제가 의미하는 것을 보여드릴게요.
Integration by Parts 기하학적으로 이해하기
우리가 함수 f(x)를 가지고 있고, x = a 및 x = b 값 사이에서 이 함수를 적분하려고 상상해 봅시다. 간단히 하기 위해, 우리가 직교 좌표 공간의 첫 번째 사분면에 모든 것을 유지한다고 상상해 봅시다. 따라서 0 ≤ a ` b입니다. f(x)가 양수이고 간단함을 위해 연속적으로 증가하는 함수라고 가정해 봅시다. 그래서 f’(x) ≥ 0입니다. 기하학적으로는, 이 적분을 수행할 때 우리는 x = a 및 x = b 사이의 f(x)의 곡선 아래 영역을 계산하는 것을 이해할 수 있습니다. 간단한 그림을 보겠습니다:
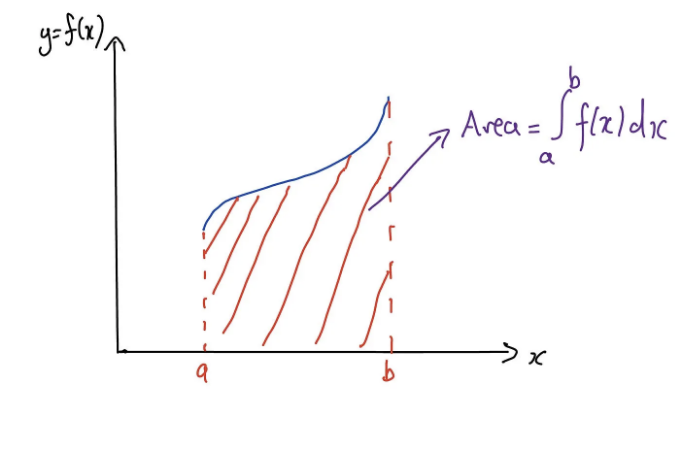
이제 또 다른 방식으로 이를 생각할 수도 있습니다. ⍺를 f(a)의 값으로, β를 f(b)의 값으로 두어 봅시다. 이제 우리는 이렇게 사진을 그릴 수 있고 몇 가지 다른 영역을 표시할 수 있습니다:
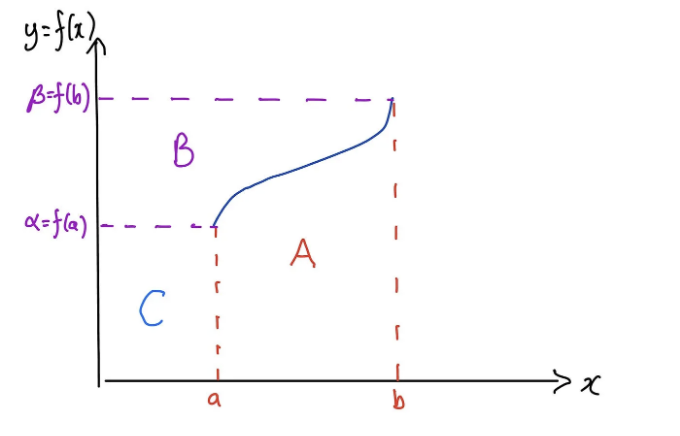
영역 A는 저희 적분의 값이며, 다른 방법으로 계산하는 방법은 큰 직사각형의 면적을 취한 다음 면적 B와 C를 뺴는 것입니다. 사실 이게 바로 부분 적분이 하는 일입니다. 이것이 어떤지 살펴봅시다.
우리의 적분(영역 A)을 다음과 같이 간단히 다시 쓰겠습니다:
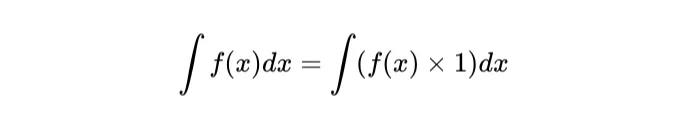
이제 v = f(x)이고 du/dx = 1인 상태에서 적분부분법을 사용하면 다음과 같습니다:
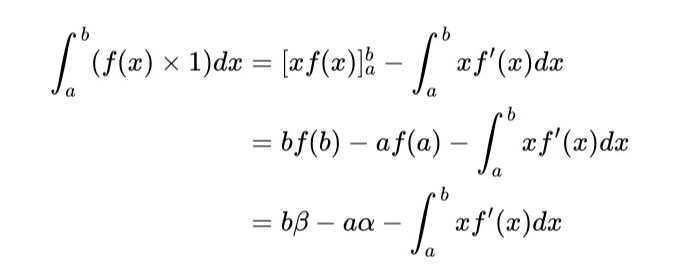
우리는 bβ가 큰 직사각형의 면적이고 a⍺는 영역 C의 면적임을 볼 수 있습니다. 이제 최종 적분을 살펴봅시다. 또한 f’(x) = dy/dx로 쓸 수 있으므로 다음과 같습니다:
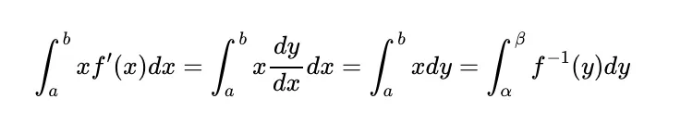
그리고 이제 이 적분이 우리 그림에서 영역 B와 동등하다는 것이 명확해졌어요. 그래서 적분 부분적으로 해석하는 것은 곡선 아래의 영역을 계산하는 간접적인 기하학적 방법으로 볼 수 있어요, 사각형의 다른 세그먼트를 빼서 관심 있는 영역이 유지되도록 하는 방식이죠. 정말 멋지죠!
고차원 예제
여러 차원으로도 이 논리를 따라갈 수 있어요. 이 적분을 고려해보세요:
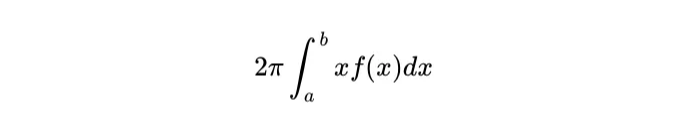
이 적분은 x축 주위에 우리의 곡선 아래 영역을 회전하여 형성된 '도넛'의 부피를 나타냅니다. 이제 동일한 적분 부분적분법을 사용하여 v = f(x) 및 du/dx = x로 도함수를 정의하면 이전 섹션과 동일한 방식으로 다음을 유도할 수 있습니다:
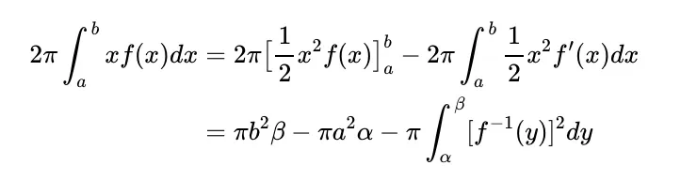
첫 항은 x축 주위에 큰 직사각형을 회전하여 형성된 원통의 부피를 나타냅니다. 두 번째 항은 y축 주위로 영역 C를 회전하여 형성된 원통의 부피를 나타내며, 마지막 적분 항은 y축 주위로 영역 B를 회전하여 형성된 부피입니다. 다시 한번, 적분 부분적분법을 이해하는 것은 원통의 부피를 취하고 세그먼트를 빼면서 회전 모양의 부피를 결정하는 간접적인 방법으로 생각할 수 있습니다.
이 적분 부분적분법의 기하학적 해설에 대해 어떻게 생각하셨나요? 자유롭게 의견을 남겨주세요!