주성분 분석(PCA)는 데이터에 대해 많은 정보를 알려줄 수 있어요. 요약하자면, 고차원 데이터셋을 시각화할 수 있는 공간으로 가져오기 위해 사용되는 차원 축소 기술입니다.

하지만 이미 알고 계시다고 가정할게요. 그렇지 않다면, 처음부터 만든 가이드를 확인해보세요.

오늘은 시각적인 부분에만 관심이 있어요. 기사를 끝까지 읽으면, 다음을 만들고 해석하는 방법을 알게 될 거에요:

PCA 시각화 사전 준비 사항

• 설명 된 분산 플롯
• 누적 설명 된 분산 플롯
• 2D/3D 구성 요소 산점도
• 속성 바이플롯
• 로딩 점수 플롯

시각화에 바로 뛰어들고 싶지만, 따라가기 위해 데이터가 필요합니다. 이 섹션에서는 데이터로드, 전처리, PCA 적합 및 일반 Matplotlib 스타일링 조정에 대해 다룹니다.

데이터 세트 정보

와인 품질 데이터셋을 사용 중이에요. Kaggle에서 무료로 이용할 수 있고, Creative Commons 라이센스로 배포되어 있어요.

Python으로 데이터셋을 불러온 후에 이렇게 보여야 해요:

import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

data = pd.read_csv("data/WineQT.csv")
data.drop(["Id"], axis=1, inplace=True)
data.head()

PCA는 평균이 0 주변에 있고 표준 편차가 1인 결측값이 없는 숫자형 특성을 전제로 해요:

X = data.drop("quality", axis=1)
y = data["quality"]

X_scaled = StandardScaler().fit_transform(X)

pca = PCA().fit(X_scaled)
pca_res = pca.transform(X_scaled)

pca_res_df = pd.DataFrame(pca_res, columns=[f"PC{i}" for i in range(1, pca_res.shape[1] + 1)])
pca_res_df.head()

데이터셋이 시각화를 위해 준비되었습니다. 그러나 만든 차트는 최상의 경우에도 끔찍해 보일 것입니다. 이를 수정해 봅시다.

Matplotlib 시각화 조정

저는 Matplotlib 스타일링 조정에 대한 포괄적인 기사를 가지고 있으니, 여기에서 깊이있는 내용을 기대하지 마세요.

내가 선택한 것은 Roboto Condensed이다)를 따라서 함께 진행하려면 TTF 글꼴을 다운로드하여 font_dir의 경로를 귀하의 운영 체제와 맞추어 바꾸세요:

import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager

import matplotlib_inline
matplotlib_inline.backend_inline.set_matplotlib_formats("svg")

font_dir = ["Roboto_Condensed"]
for font in font_manager.findSystemFonts(font_dir):
    font_manager.fontManager.addfont(font)

plt.rcParams["figure.figsize"] = 10, 6
plt.rcParams["axes.spines.top"] = False
plt.rcParams["axes.spines.right"] = False
plt.rcParams["font.size"] = 14
plt.rcParams["figure.titlesize"] = "xx-large"
plt.rcParams["xtick.labelsize"] = "medium"
plt.rcParams["ytick.labelsize"] = "medium"
plt.rcParams["axes.axisbelow"] = True
plt.rcParams["font.family"] = "Roboto Condensed"

이제 모던한 고해상도 차트를 플로팅할 때마다 얻게 될 것입니다.

PCA 시각화를 시작하는 데 필요한 모든 것이 이것입니다. 그럼 첫 번째로 들어가 봅시다.

PCA Plot #1: 설명된 분산 그래플

질문: 각 주성분이 데이터의 총 분산 중 얼마를 설명하나요?

같은 궁금증을 가졌다면, 이 그래프를 확인해보세요. 일반적으로 처음 몇 개의 주성분이 전체 분산의 상당 부분을 설명하지만, 이는 시작하는 피처의 개수에 따라 다를 수 있습니다.

5개의 피처를 가진 데이터셋의 첫 번째 주성분은 500개의 피처를 가진 데이터셋의 첫 번째 주성분보다 더 많은 총 분산을 설명할 것입니다 — 당연한 얘기네요!

plot_y = [val * 100 for val in pca.explained_variance_ratio_]
plot_x = range(1, len(plot_y) + 1)

bars = plt.bar(plot_x, plot_y, align="center", color="#1C3041", edgecolor="#000000", linewidth=1.2)
for bar in bars:
    yval = bar.get_height()
    plt.text(bar.get_x() + bar.get_width() / 2, yval + 0.001, f"{yval:.1f}%", ha="center", va="bottom")

plt.xlabel("주성분")
plt.ylabel("설명된 분산의 백분율")
plt.title("주성분별 설명된 분산", loc="left", fontdict={"weight": "bold"}, y=1.06)
plt.grid(axis="y")
plt.xticks(plot_x)

plt.show()

이 그림은 11개의 특성에서 총 분산의 28.7%가 단일 주성분으로 설명되는 것을 보여줍니다. 다시 말해, 데이터 세트 전체를 단일 선 (1차원)으로 그릴 수 있고 여전히 변이의 약 1/3을 보여줄 수 있습니다.

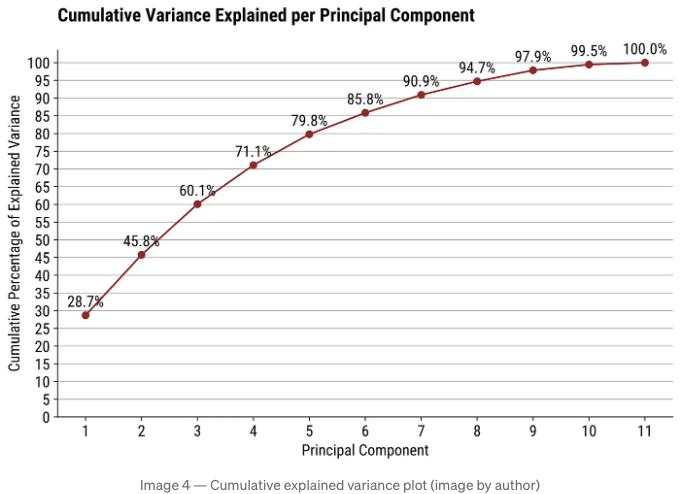
PCA 플롯 #2: 누적 설명된 분산 플롯

질문: 데이터의 차원을 줄이고 싶지만, 분산의 적어도 90%는 유지하고 싶어요. 어떻게 해야 하나요?

가장 간단한 해답은 설명된 분산의 누적 합을 보여주도록 첫 번째 차트를 수정하는 것입니다. 코드에서는 현재 항목까지의 값을 반복적으로 더하면 됩니다.

exp_var = [val * 100 for val in pca.explained_variance_ratio_]
plot_y = [sum(exp_var[:i+1]) for i in range(len(exp_var))]
plot_x = range(1, len(plot_y) + 1)

plt.plot(plot_x, plot_y, marker="o", color="#9B1D20")
for x, y in zip(plot_x, plot_y):
    plt.text(x, y + 1.5, f"{y:.1f}%", ha="center", va="bottom")

plt.xlabel("Principal Component")
plt.ylabel("Cumulative Percentage of Explained Variance")
plt.title("Cumulative Variance Explained per Principal Component", loc="left", fontdict={"weight": "bold"}, y=1.06)

plt.yticks(range(0, 101, 5))
plt.grid(axis="y")
plt.xticks(plot_x)

plt.show()

요즘 세대조사(PCA) 플롯 #3: 2D/3D 컴포넌트 산점도

질문: 고차원 데이터셋의 레코드 간 관계를 시각화하는 방법이 무엇인가요? 한 번에 3개 이상의 차원을 볼 수 없어요.

첫 번째 2개나 3개 주성분의 산점도가 찾고 있는 것입니다. 이상적으로, 데이터 포인트를 대상 변수의 서로 다른 값으로 색상 표시해야 합니다(분류 데이터셋을 가정합니다).

같이 살펴보겠습니다.

2D 산점도

처음 두 성분은 분산의 약 45%를 설명합니다. 만족스러운 양이지만, 2차원 산점도로는 여전히 절반 이상을 설명할 수 없습니다. 기억해 두시는 것이 좋습니다.

total_explained_variance = sum(pca.explained_variance_ratio_[:2]) * 100
colors = ["#1C3041", "#9B1D20", "#0B6E4F", "#895884", "#F07605", "#F5E400"]

pca_2d_df = pd.DataFrame(pca_res[:, :2], columns=["PC1", "PC2"])
pca_2d_df["y"] = data["quality"]

fig, ax = plt.subplots()
for i, target in enumerate(sorted(pca_2d_df["y"].unique())):
    subset = pca_2d_df[pca_2d_df["y"] == target]
    ax.scatter(x=subset["PC1"], y=subset["PC2"], s=70, alpha=0.7, c=colors[i], edgecolors="#000000", label=target)

plt.xlabel("주성분 1")
plt.ylabel("주성분 2")
plt.title(f"와인 품질 데이터셋 PCA ({total_explained_variance:.2f}% 설명된 분산)", loc="left", fontdict={"weight": "bold"}, y=1.06)

ax.legend(title="와인 품질")
plt.show()

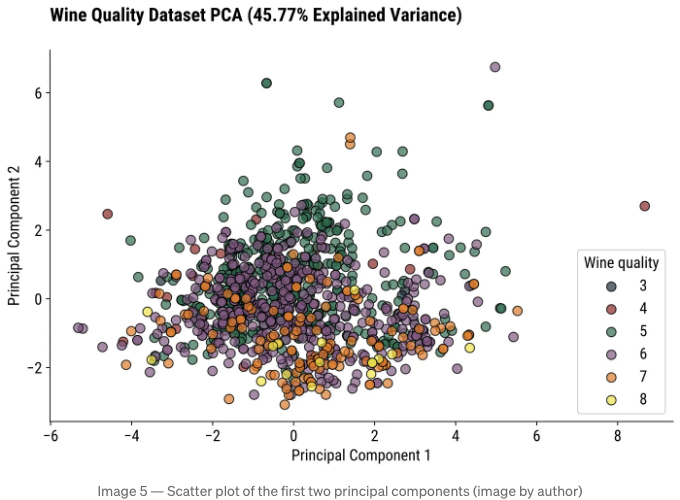
혼란스러워 보이죠, 그래서 차원을 하나 추가해보겠습니다.

3D 산점도

추가 차원은 설명된 분산을 약 60%로 늘릴 것입니다. 3D 차트는 보는 데 더 어렵고, 해석은 차트의 각도에 약간 따라 달릴 수 있음을 염두에 두세요.

total_explained_variance = sum(pca.explained_variance_ratio_[:3]) * 100
colors = ["#1C3041", "#9B1D20", "#0B6E4F", "#895884", "#F07605", "#F5E400"]

pca_3d_df = pd.DataFrame(pca_res[:, :3], columns=["PC1", "PC2", "PC3"])
pca_3d_df["y"] = data["quality"]

fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection="3d")

for i, target in enumerate(sorted(pca_3d_df["y"].unique())):
    subset = pca_3d_df[pca_3d_df["y"] == target]
    ax.scatter(xs=subset["PC1"], ys=subset["PC2"], zs=subset["PC3"], s=70, alpha=0.7, c=colors[i], edgecolors="#000000", label=target)

ax.set_xlabel("Principal Component 1")
ax.set_ylabel("Principal Component 2")
ax.set_zlabel("Principal Component 3")
ax.set_title(f"Wine Quality Dataset PCA ({total_explained_variance:.2f}% Explained Variance)", loc="left", fontdict={"weight": "bold"})

ax.legend(title="Wine quality", loc="lower left")
plt.show()

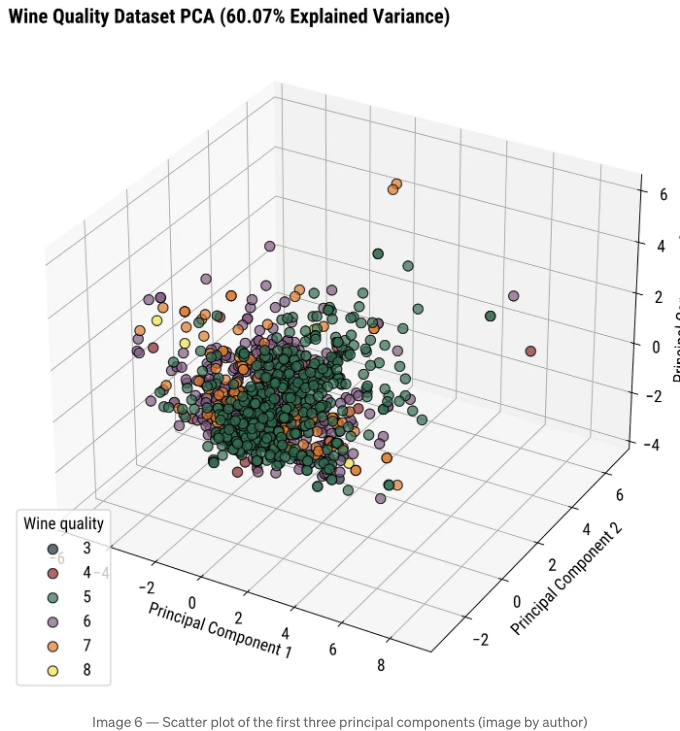
To change the perspective, you can play around with the view_init() function. It allows you to change the elevation and azimuth of the axes in degrees:

ax.view_init(elev=<value>, azim=<value>)

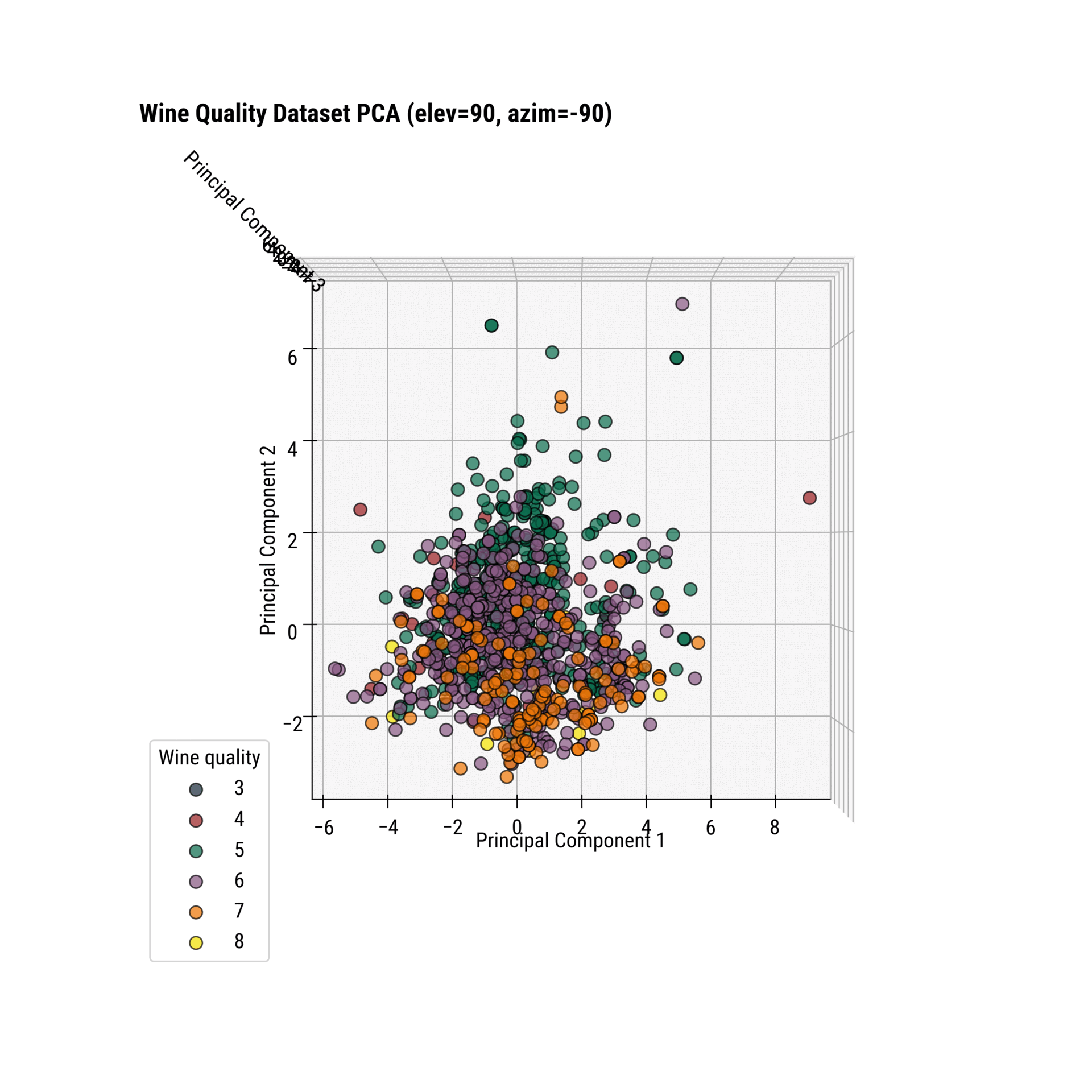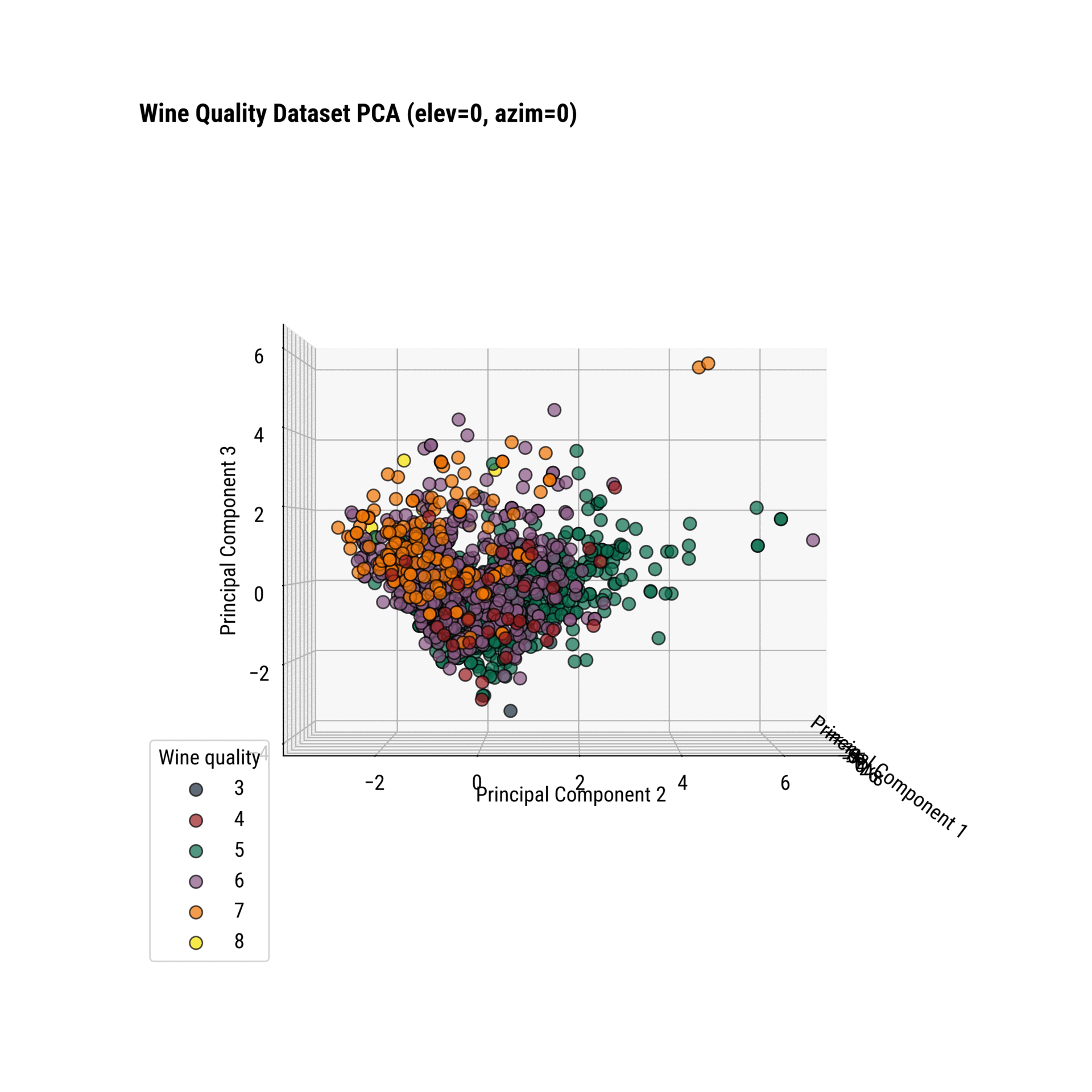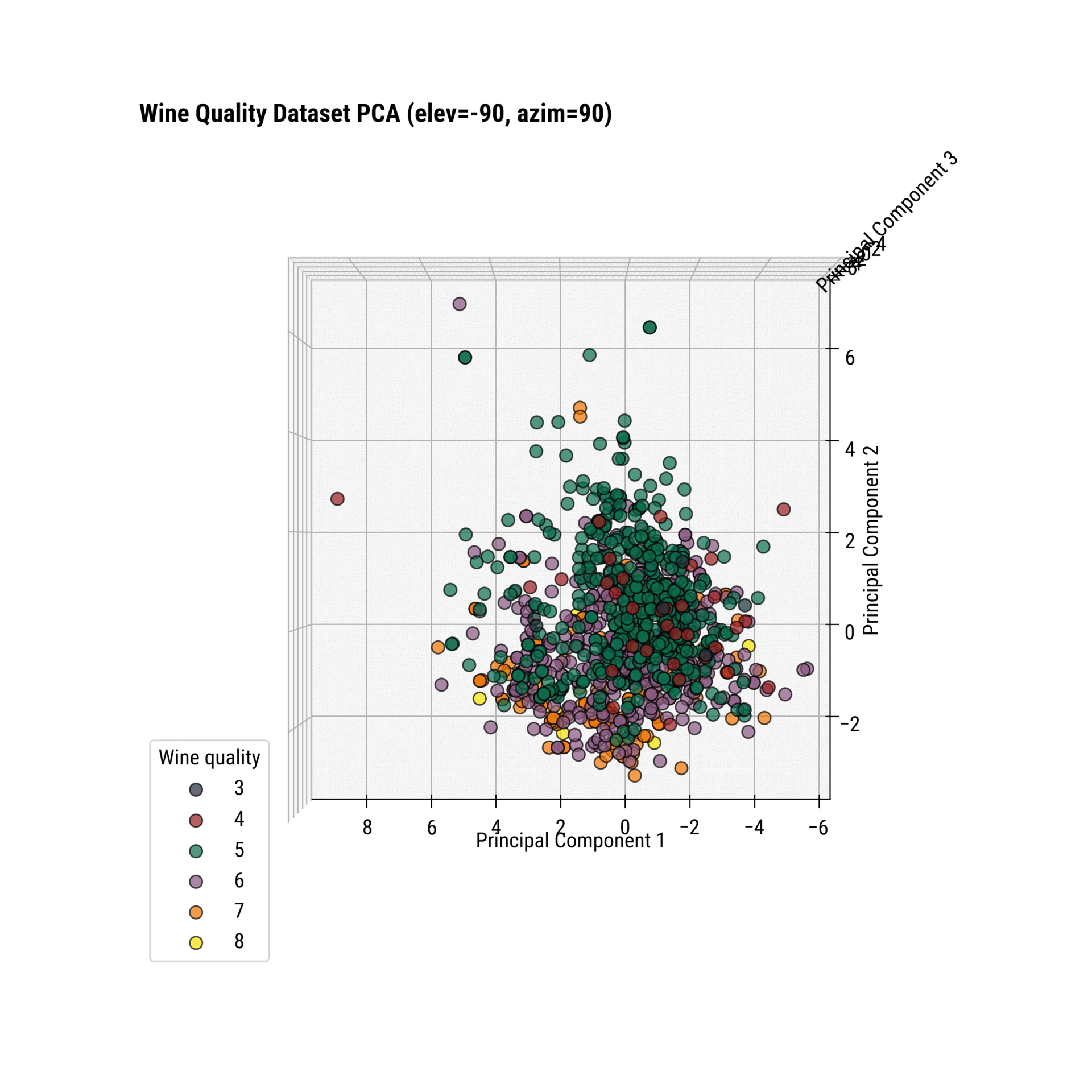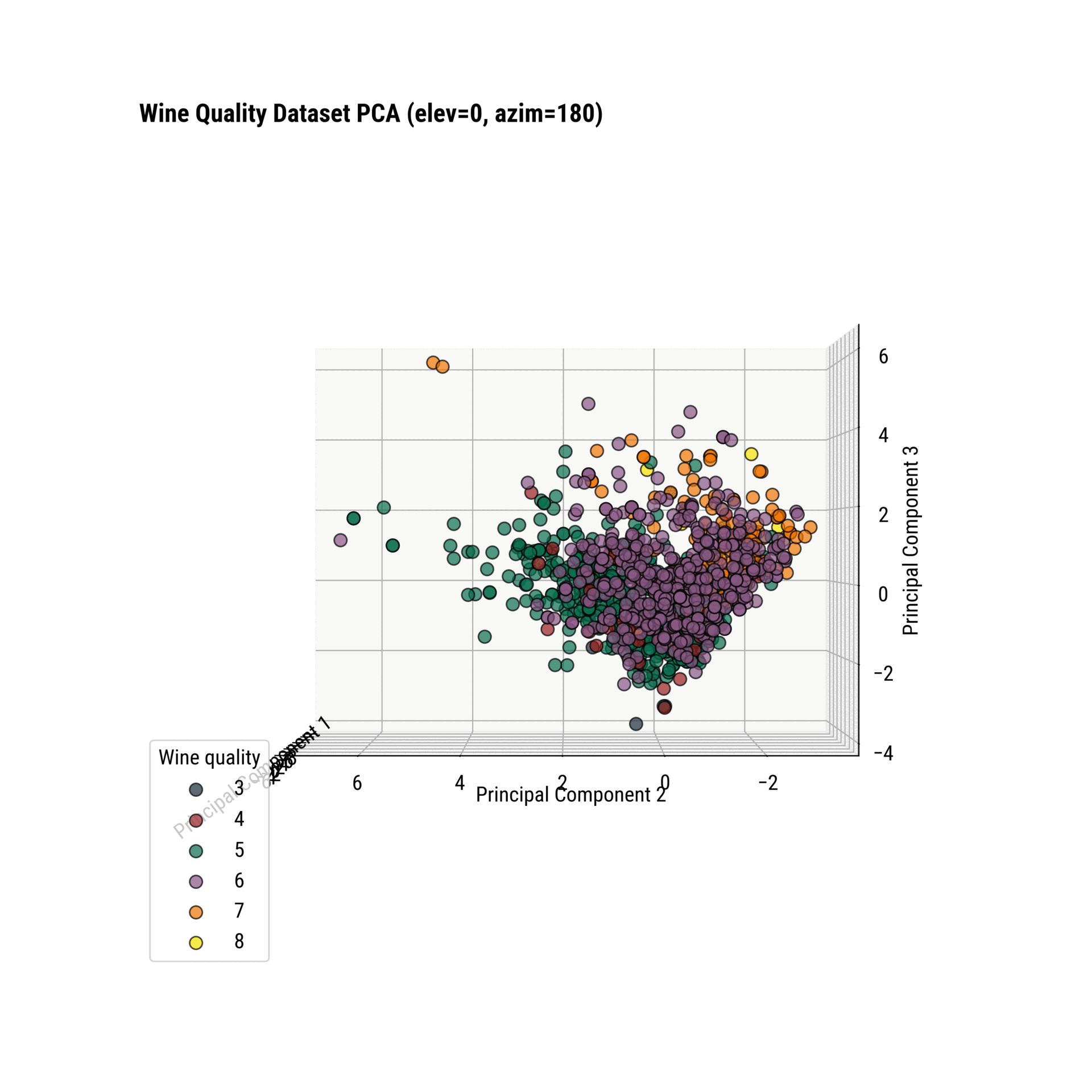
Or, you can use an interactive charting library like Plotly and rotate the chart like a sane person.

PCA Plot #4: Biplot

Question: Can I see how the original variables contribute to and correlate with the principal components?

그래. 짜증나게도 이 차트 유형은 R에서 만드는 게 훨씬 쉽지만, 어쩔 수 없지.

labels = X.columns
n = len(labels)
coeff = np.transpose(pca.components_)
pc1 = pca.components_[:, 0]
pc2 = pca.components_[:, 1]

plt.figure(figsize=(8, 8))

for i in range(n):
    plt.arrow(x=0, y=0, dx=coeff[i, 0], dy=coeff[i, 1], color="#000000", width=0.003, head_width=0.03)
    plt.text(x=coeff[i, 0] * 1.15, y=coeff[i, 1] * 1.15, s=labels[i], size=13, color="#000000", ha="center", va="center")

plt.axis("square")
plt.title(f"Wine Quality Dataset PCA Biplot", loc="left", fontdict={"weight": "bold"}, y=1.06)
plt.xlabel("Principal Component 1")
plt.ylabel("Principal Component 2")

plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.xticks(np.arange(-1, 1.1, 0.2))
plt.yticks(np.arange(-1, 1.1, 0.2))

plt.axhline(y=0, color="black", linestyle="--")
plt.axvline(x=0, color="black", linestyle="--")
circle = plt.Circle((0, 0), 0.99, color="gray", fill=False)
plt.gca().add_artist(circle)

plt.grid()
plt.show()

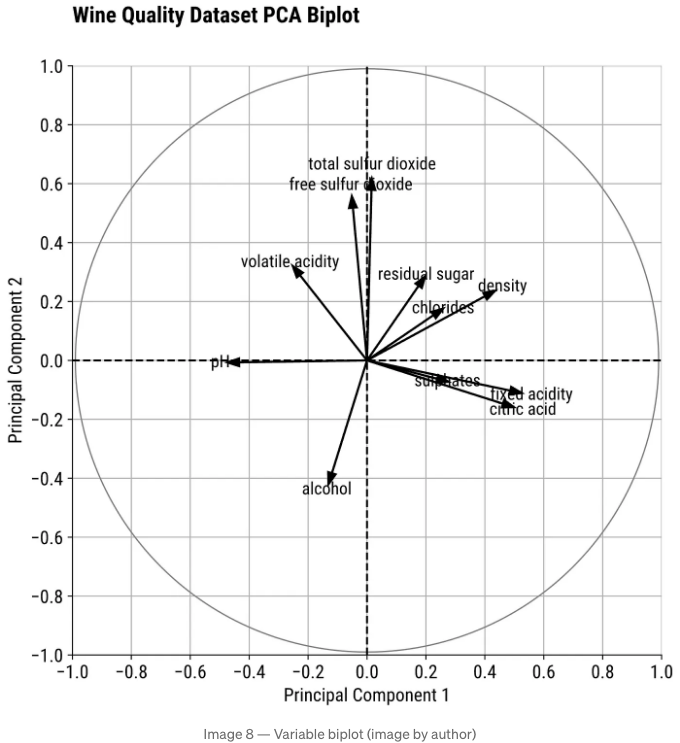
그러니까, 뭐를 보고 계신 건가요? 바이플롯을 해석할 때 알아야 할 내용이에요:

• 화살표 방향: 해당 변수가 주성분과 어떻게 일치하는지를 나타냅니다. 같은 방향을 향하는 화살표는 양의 상관 관계가 있습니다. 반대 방향을 향하는 화살표는 음의 상관 관계가 있습니다.
• 화살표 길이: 변수가 주성분에 얼마나 기여하는지를 나타냅니다. 더 긴 화살표는 더 강한 기여를 나타냅니다 (해당 변수가 더 많은 분산을 설명합니다). 더 짧은 화살표는 더 약한 기여를 나타냅니다 (해당 변수가 덜 설명되는 분산을 차지합니다).
• 화살표 사이의 각도: 0º는 완벽한 양의 상관 관계를 나타냅니다. 180º는 완벽한 음의 상관 관계를 나타냅니다. 90º는 상관 관계가 없음을 나타냅니다.

위 차트를 통해 황산염, 고정산도 및 구연산이 상관 관계가 높음을 확인할 수 있습니다.

PCA Plot #5: Loading Score Plot

질문: 원본 데이터 세트의 어떤 변수가 각 주성분에 가장 큰 영향을 미칩니까?

로딩 스코어를 시각화하여 원래 변수의 가중치가 주성분에 얼마나 영향을 미치는지 확인할 수 있어요. 높은 절대값은 더 높은 영향을 나타냅니다.

이는 주성분과의 상관 관계로, -1부터 +1까지의 범위를 갖고 있어요. 주로 방향보다는 크기에 중점을 둘 거예요.

로딩 = pd.DataFrame(
    data=pca.components_.T * np.sqrt(pca.explained_variance_), 
    columns=[f"PC{i}" for i in range(1, len(X.columns) + 1)],
    index=X.columns
)

fig, axs = plt.subplots(2, 2, figsize=(14, 10), sharex=True, sharey=True)
colors = ["#1C3041", "#9B1D20", "#0B6E4F", "#895884"]

for i, ax in enumerate(axs.flatten()):
    explained_variance = pca.explained_variance_ratio_[i] * 100
    pc = f"PC{i+1}"
    bars = ax.bar(로딩.index, 로딩[pc], color=colors[i], edgecolor="#000000", linewidth=1.2)
    ax.set_title(f"{pc} 로딩 스코어 ({explained_variance:.2f}% 설명된 분산)", loc="left", fontdict={"weight": "bold"}, y=1.06)
    ax.set_xlabel("특성")
    ax.set_ylabel("로딩 스코어")
    ax.grid(axis="y")
    ax.tick_params(axis="x", rotation=90)
    ax.set_ylim(-1, 1)
    
    for bar in bars:
        yval = bar.get_height()
        offset = yval + 0.02 if yval > 0 else yval - 0.15
        ax.text(bar.get_x() + bar.get_width() / 2, offset, f"{yval:.2f}", ha="center", va="bottom")

plt.tight_layout()
plt.show()

첫 번째 주성분이 전반적인 변동성의 약 29%를 설명하고 고정 산도 특성의 로딩 스코어가 높은 경우(0.86), 이는 중요한 특성이며 추가 분석과 예측 모델링에 유지해야 함을 의미합니다.

이렇게 하면 점수를 불러와 특성 선택 기술로 사용할 수 있습니다.

Python PCA 시각화 요약

결론적으로 PCA는 차원을 축소하고 통찰을 얻기 위한 반드시 알아야 하는 기술입니다. 우리 인간은 긴 숫자 목록을 해석하는 데 어려움을 겪기 때문에 시각화가 유용합니다.

PCA 덕분에 2D/3D 차트로 고차원 데이터셋을 시각화할 수 있습니다. 그 과정에서 일부 분산을 잃게 되므로 시각화를 신중하게 해석해야 합니다.

어떤 PCA 시각화를 데이터 과학 프로젝트에서 사용하시나요? 아래 댓글란에 꼭 알려주세요.

파이썬, 데이터 과학, 기계 학습에 관한 독점 콘텐츠를 받으려면 제 뉴스레터에 가입해주세요.

원문은 https://darioradecic.substack.com에서 확인하실 수 있습니다.