선형 프로그래밍을 사용하여 전 세계적으로 완벽한 컨테이너 기반 공급망 운영을 최적화하기

최근에 브라질의 대규모 기업을 위해 세계적으로 상품과 서비스를 판매하는 프로젝트에 동료의 초대를 받았습니다.

해당 프로젝트는 운송 최적화를 다루는 것으로 매우 흥미로웠으며 도전적이었습니다. 그래서 이에 대해 어떻게 문제를 해결했는지와 라이브러리 cvxpy를 사용하여 문제를 해결한 경험에 대해 쓰고 싶습니다. (Tesla, Netflix 및 Two Sigma와 같은 기업에서 최적화 문제 해결에 사용됨).

구체적으로 이 게시물은 다음을 다룹니다:

다양한 제약 조건을 가지고 전 세계적으로 컨테이너를 운송하는 도전
회사의 데이터를 어떻게 관리했고, 선형 변환 집합으로 설명했는지
변수와 제약 조건을 선형 프로그래밍 공식에 맞게 적응시키는 방법
목적 함수와 제약 조건이 볼록(convex)하다고 보장하는 데 사용된 기술 — cvxpy의 주된 제약사항

이제 더 이상 말이 필요하지 않습니다. 시작해봅시다.

1. 도전과제

프로젝트가 시작될 때, 회사는 이미 Microsoft Excel Solver 위에 구현된 솔루션이 있다는 것을 알려주었습니다. Solver는 운송비, 화물, 저장 및 운영 비용을 줄이려는 목표를 가지고 일련의 제약 조건을 따르면서 컨테이너를 가장 효율적으로 관리하는 방법을 최적화하는 것이 목적이었습니다.

해결책은 잘 작동했지만 영업이 확대되면서 프로세스가 중단되고 병목 현상으로 고통받기 시작했다고 회사에서 설명했습니다. 때때로 할당해야 할 컨테이너가 너무 많아서 솔버가 전체 데이터 집합을 처리하고 답변을 내기까지 몇 일이 걸릴 수 있었습니다.

그들은 시스템의 업무 부담을 다룰 수 있는 새로운 것을 개발해 달라고 요청했으며 동시에 시스템이 요구에 따라 새로운 제약 조건을 수용할 수 있도록 충분히 유연해야 했습니다.

먼저 회사는 전국에 공장이 분포되어 있고 각 공장에서 수요에 따라 컨테이너가 준비됩니다:

각 공장은 자체 수요에 따라 매주 컨테이너를 생산하며, 따라서 일부 공장은 다른 공장들보다 더 많은 컨테이너를 생산할 것입니다. 각 컨테이너는 자체 상품을 운반하기 때문에 판매 가격도 변동됩니다 (이 변수는 곧 중요해질 것입니다).

각 컨테이너의 운명 또한 다양합니다. 어떤 컨테이너는 인접 국가로 운반되고, 다른 컨테이너는 세계 각국으로 이동해야 합니다. 따라서 회사는 컨테이너를 적절한 부두로 보내야 하며, 그렇지 않으면 각 국가의 부두 간 연결이 부족하여 배송에 실패할 수 있습니다.

공장을 적절한 부두에 연결시키려고 할 때 여러 새로운 변수가 나타납니다. 먼저, 각 공장은 컨테이너를 운송하는 방법을 선택할 수 있습니다: 기차를 이용하거나 — 이 경우 선택할 수 있는 다양한 종류의 계약이 있습니다 — 혹은 트럭을 이용합니다 (또한 다양한 종류의 계약을 선택할 수도 있습니다):

이제 또 다른 도전이 등장했습니다: 각 컨테이너에는 특정 목적지가 있고 각 부두의 이용 가능한 선박에도 목적지가 있습니다. 따라서 목적지는 반드시 일치해야 합니다! 홍콩으로 가야 할 컨테이너를 아시아로 가지 않는 부두로 운반하면 전체 컨테이너를 희생시킨 셈이 됩니다.

이 일치하는 문제는 때로 공장들이 브라질과 세계의 나머지 사이의 연결을 만드는 유일한 선택지로서 더 먼 부두로 컨테이너를 운송해야 하는 경우가 있음을 의미합니다 (이는 더 많은 비용이 들 수도 있습니다). 선사들은 다른 변수가 되며, 각 선박의 여유 공간 및 선박의 목적지에 대한 가용성을 고려해야 합니다.

선사들은 "과잉 예약 공간"이라고 하는 것도 허용할 수 있습니다. 항공편에 해당하는 개념처럼, 선박에도 해당되지만 여기서는 개념이 조금 더 제한적이지 않습니다. 주어진 주에 대해 선사들은 "과잉 예약 요인"을 알려줄 수 있으며, 이를 통해 각 선박에 임계 용량을 초과하는 얼마나 더 많은 컨테이너를 추가할 수 있는지에 대한 개념을 얻을 수 있습니다 — 기대한대로 화물이 더 비싸집니다. 최적화자는 이 요인을 사용하여 남은 컨테이너를 할당하고 더 저렴한 운송을 활용할 수 있습니다.

옵티마이저는 따를 규칙 세트도 고려해야 해요. 이곳에는 준수해야 할 요구 사항 요약이 있어요:

선박에는 최대 수용능력이 있어요: 각 선박은 "거래"를 통해 특정 지역에 서비스를 제공해요. 각 선사는 각 거래마다 컨테이너의 최대 수용 능력을 가지고 있어요 — 이 규칙은 때때로 오버부킹을 통해 위반될 수도 있어요.
공장과 도크 연결: 공장은 유효하고 이용 가능한 교통수단이 있는 도크로만 컨테이너를 보낼 수 있어요 — 공장이 특정 도크에 기차역 연결이 없다면 옵티마이저는 다른 교통수단을 선택해야 해요.
교통량 제한: 회사는 교통에 사용 가능한 계약 및 슬롯이 변할 수 있다고 명확히 밝혔어요; 매달 일정 슬롯을 기차로 사용할 수 있는 라이선스와 협정이 있어서 이는 컨테이너 수에 상한선을 더해요.
출발 도크와 선사 연결: 옵티마이저는 선사가 승선 가능한 선박 상에 공간을 가지고 송장하는 공장에서 컨테이너를 보내야하고, 컨테이너가 이동하는 교역에 참석해야 해요.
오버부킹: 오버부킹은 발생할 수 있어요 — 우리의 대체 기회 같은 것이죠. 각 선사는 최대용량을 넘는 여유 슬롯을 얼마나 사용할 수 있는지에 대한 요인을 가지고 있어요. 오버부킹 된 컨테이너는 훨씬 비싸지고, 이는 이미 사용 가능한 모든 공간이 이미 사용되었을 때에만 발생해야 해요.
운송 또는 비운송: 옵티마이저는 주어진 컨테이너를 운송하는 것보다 공장에 저장하는 것이 더 나은지 결론 짓을 수도 있어요. 이는 총 비용의 예상에 영향을 미쳐요.

우리는 이미 도착한 걸까요? 음, 정확히 그렇지는 않아요. 실제로는 도전 과제가 약간 더 복잡해요. 각 컨테이너를 운송하는 데 공장이 얼마나 걸리는지와 언제 선사가 도크에서 이용 가능할지 연결해야 해요. 너무 느린 운송수단을 선택하면 선박을 놓칠 수 있고, 동일한 목적지로 가는 다른 선박이 있다는 희망으로 기다려야 할 수도 있고, 기본적으로는 컨테이너를 잃게 될 수도 있어요. 이 게시글은 시간 변수를 고려하지 않으므로 개발을 훨씬 복잡하게 만들어요.

도전 과제를 가지고 있으니, 이제 이 문제를 어떻게 해결했는지 살펴볼까요? 🥷!

3. 선형 프로그래밍

선형 프로그래밍(LP)은 선형 변환으로 표현된 제약 조건 집합을 수용하는 최적화 기술입니다.

수학적으로는 다음과 같은 것이 있습니다:

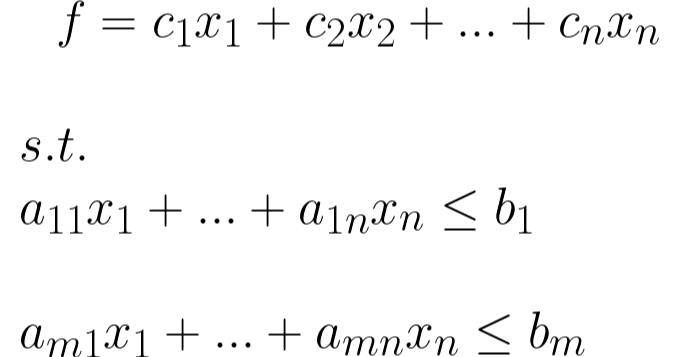
Linear Programming

f는 목적 함수(또는 비용 함수)이며, 이 도전에서는 각 운송, 선박에 연관된 비용을 나타내며 컨테이너가 초과 예약 상태로 저장되었는지, 공장에 컨테이너를 남겨 둘 지 여부에 대한 트레이드오프를 나타냅니다.

x 값은 최적화자가 목적을 최소화하기 위해 조작해야 하는 변수를 나타냅니다. 우리의 경우, Transport, Ship, Dock 및 초과 예약 상태를 선택해야 합니다.

이 개념을 더 구체적으로 만들고 이 게시물의 주요 도전과 연결시키기 위해 cvxpy 위에 매우 간단한 구현부터 시작해 보겠습니다.

3.1 간단한 예제

다음과 같은 설정이 있다고 가정해 봅시다:

회사는 특정 주에 동일한 공장에서 4개의 컨테이너를 생산했습니다. 그 값은 [$200, $300, $400, $500] 입니다.
공장은 한 번에 한 종류의 운송 수단만 사용할 수 있습니다.
공장은 한 개의 부두에만 연결되어 있습니다.
이 가정된 주에 두 개의 선사가 부두에서 이용 가능한 배를 보유하고 있습니다. 각각 컨테이너 당 $100과 $130을 청구합니다.
첫 번째 선주는 2개의 남은 슬롯을 가지고 있고, 두 번째 선주는 딱 1개만 가지고 있습니다.

최적화 프로그램의 주요 목표는 4개의 컨테이너를 배의 이용 가능한 공간에 분배하면서 총 운송 비용을 최소화하는 것입니다.

그렇다면 cvxpy에서 어떻게 구현할까요? 실은 매우 간단합니다. 먼저, 최적화 프로그램이 할 수 있는 선택을 나타내는 변수 x가 필요합니다. 이 경우 x를 가장 좋은 방법으로 나타내는 방법은 모양이 (4, 2)인 부울 배열로 표시하는 것입니다. 여기서 각 행은 특정 컨테이너에 해당하고, 2개의 열은 2개의 이용 가능한 선사와 대응합니다:

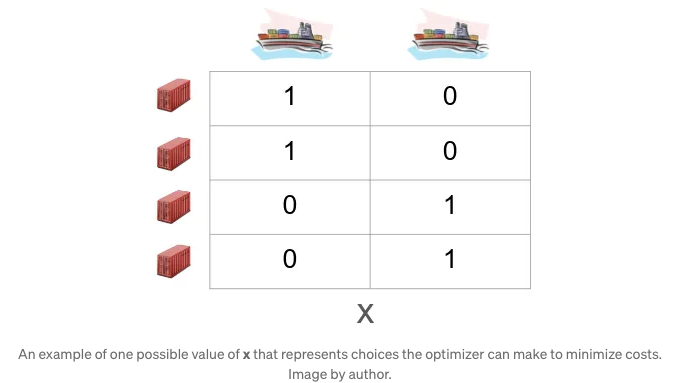
HowWeOptimizedTheProblemOfGlobalContainersDistribution_4

해당 표의 행에서 “1”의 값은 최적화자가 해당 열의 선하에 해당 컨테이너를 할당했음을 의미합니다. 이 예에서 첫 번째와 두 번째 컨테이너가 첫 번째 선하에, 그리고 세 번째와 네 번째 컨테이너가 두 번째 선하에 각각 할당됩니다. 각 행에는 하나의 값만 포함될 수 있으며 다른 값은 “0”이어야 합니다. 그렇지 않으면 특정 컨테이너가 동시에 두 선하에 할당되었다는 뜻이 되어 잘못된 결과를 초래할 수 있습니다.

따라서 최적화자의 도전은 요구 사항을 준수하면서 이 배열을 계속 바꿔가며 총 비용을 최소화하는 것입니다.

비용은 선하와 컨테이너 자체에 해당하는 두 부분으로 구성됩니다. 특정 컨테이너가 어떤 선하에도 할당되지 않으면 해당 비용이 최종 비용에 추가됩니다. 따라서 $500의 컨테이너보다 $200의 컨테이너를 우선으로 할당하는 것이 더 나은 선택입니다.

코드 구현에 대해 이 가능성이 있습니다:

고려해야 할 주요 포인트:

cvxpy에서는 변수 집합, 제약 조건 및 마지막으로 비용 표현식이 필요합니다.
코드 constraint0 = cx.sum(x_shippers, axis=1) = 1은 최적화 중인 x가 준수해야 하는 제약 조건입니다. 일반적으로 최적화 과정을 유지하기 위해 꼭 convexe해야 하며(수렴을 보장), 등식 표현이나 상한 등식이 될 수 있습니다. 이 경우 sum 연산자는 axis=1에 적용되어 "열별 합"을 의미합니다. 이 규칙은 x_shippers의 각 행의 합이 최대 1 이하일 수 있다는 것을 의미하며, 특정 컨테이너가 동시에 여러 선박에 할당되지 않도록 보장합니다. 합 제약 조건이 = 규칙을 따르므로 특정 행은 모두 0일 수 있습니다. 즉, 특정 컨테이너가 어떤 선박에도 할당되지 않을 수 있습니다(예: 선박의 가용 공간 부족 등).
constraint1 = cx.sum(x_shippers, axis=0) = shippers_spaces 역시 constraint0과 유사하게 작동합니다. 각 선박에 할당된 모든 컨테이너가 최대 용량을 초과해서는 안 된다는 것을 의미합니다.
그리고 문제의 핵심으로 접근합니다: 비용 함수. 다음과 같이 정의됩니다: cost = cx.sum(x_shippers @ shippers_cost.T) + container_costs @ (1 - cx.sum(x_shippers, axis=1)). 첫 번째 구성 요소인 cx.sum(x_shippers @ shippers_cost.T)는 각 컨테이너를 각 선박에 할당하는 데 필요한 모든 비용을 나타냅니다. “@”는 dot product를 나타내므로 연산 결과는 이미 각 컨테이너에 할당된 비용입니다. 이 비용을 총 비용을 위해 합산해야 합니다. 두 번째 구성 요소인 container_costs @ (1 - cx.sum(x_shippers, axis=1))는 더 흥미로울 수 있습니다. 여기서 cvxpy에서 문제를 표현하는 데 사용할 수 있는 전략을 볼 수 있습니다. 1에서 행 값을 표현한 cx.sum(x_shippers, axis=1)를 뺀 행렬을 사용하면 사용 여부를 나타내는 (4, 1) 행렬을 얻습니다. 선박화되지 않은 컨테이너 추적을 위해 미선택 컨테이너의 비용 값을 합산합니다.

이것은 결과의 예시입니다:

print(x_shippers.value)
array([[0., 0.], [0., 1.], [1., 0.], [1., 0.]])

0번 컨테이너는 배에 할당되지 않았습니다(가장 저렴하기 때문에 우선순위가 되지 않았습니다).

계속하기 전에 몇 가지 팁을 알려드리겠습니다:

Colab에서 cvxpy를 사용하여 실험을 실행할 수 있습니다. 단순히 !pip install cvxpy를 실행하면 거의 준비됩니다.
모델을 구현할 때 올바른 경로에 있는지 확인하기 위해 몇 가지 확인을 실행할 수 있습니다. 저는 사용하는 기술 중 하나로 변수에 초기값을 설정하는 것을 좋아합니다. 예를 들어 x_shippers = cx.Variable((2, 2), value=[[1, 0], [0, 1]])와 같이 초기값을 설정한 후, 작업을 실행한 후(r=A @ x_shippers와 같은), 예상대로 모든 것이 작동하는지 확인하기 위해 결과 r.value 속성을 인쇄할 수 있습니다.
cvxpy를 사용할 때 최적화를 실행할 때 때로는 오류가 발생합니다. 오류 메시지 중 일반적인 문제는 다음과 같습니다:

이것은 유명한 DCP (Disciplined Convex Problem의 약자)입니다. 이는 제약과 목적을 볼록으로 보장하기 위해 따라야 하는 규칙 집합으로 구성되어 있습니다. 예를 들어, 합산 연산자 대신 최댓값을 사용하면 정확히 동일한 결과가 나오지만 실행하려고하면 DCP 에러가 발생합니다. DCP는 비용과 제약 조건을 표현하는 데 사용되는 모든 작업이 볼록성 규칙을 따라야 함을 의미합니다.

이전 예제는 cvxpy API에 대한 간단한 소개로 잘 작동합니다. 이제 같은 주제의 조금 더 진화된 문제를 고려해 봅시다.

3.2 중간 예제

"같은 비용과 조건을 갖는 4개의 컨테이너를 다시 고려해 봅시다. 이번에는 첫 번째와 세 번째 컨테이너가 목적지 '0'으로 가야 하고 두 번째와 네 번째 컨테이너는 목적지 '1'로 가야 하며 이용 가능한 공간은 이전과 동일합니다 ([2, 1]). 이 문제에 대한 입력은 다음과 같을 것입니다:

모든 컨테이너는 동일한 공장에서 생산되지만, 이번에는 기차와 트럭을 이용한 두 가지 옵션이 있습니다. 각각의 비용은 [$50, $70]입니다. 이번 주에는 최대 2개의 컨테이너를 기차에 할당할 수 있을 것입니다.

계속하기 전에, 이 문제를 어떻게 해결할지 생각해 보세요. 선형 프로그래밍 작업에 권장되는 필수 단계를 기억해 보세요:"

어떤 변수들이 문제를 설명하는 데 필요한가요? x_shippers = ...
비용 함수를 어떻게 표현하죠? cost = ...
행렬과 수학적 연산을 통해 제약 조건을 어떻게 사용하나요? destines `= x_shippers...

(시도해보기 위해 Colab을 사용할 수도 있습니다)

…

머리 기호를 사용해 주세요.

표 태그를 마크다운 형식으로 변경해주세요.

...

다음은 가능한 한 가지 해결책입니다:

전반적으로 이전과 동일한 구조를 따릅니다. 코드에 대한 몇 가지 참고 사항:

이제는 x_shippers와 x_transport 두 변수를 최적화하고 있어요.
기차에 대한 매퍼와 선적인을 목적지에 매핑하는 데 사용해요. 매퍼 변수의 이름은 우리의 규칙에 따라 행 공간의 변수 이름으로 시작하고 열을 따라 이어져요. 예를 들어, destine_shippers는 행이 목적지를 나타내고 열이 선적인을 나타냅니다. 구체적으로, dest_ships_arr = destine_shippers_map[containers[:, 1]]의 결과는 각 컨테이너의 목적지를 방문하는 선박을 포함하는 4행의 행렬이에요. 더 명확하게 하기 위해:

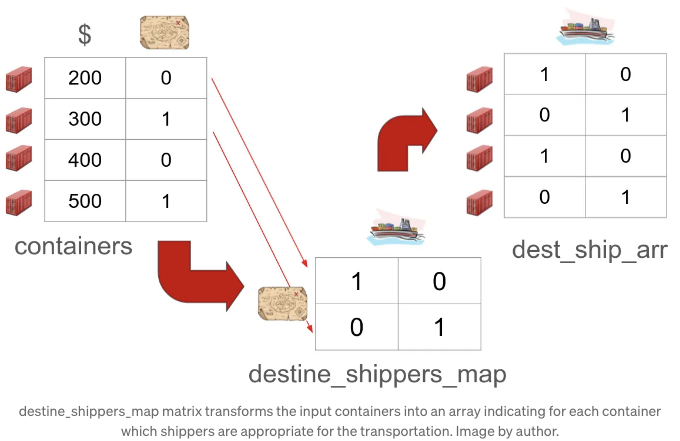
매퍼는 입력 데이터를 제약 조건 및 비용 함수에 사용할 수 있게 도와줘요. 이전 예시에서 최적화기는 예를 들어 첫 번째 컨테이너에 선적인 0을 할당하고 두 번째 컨테이너에 선적인 1을 할당하는 것으로 제한되어 있어요. 이것은 다음과 같이 구현되어 있어요: constraint02 = x_shippers `= dest_ships_arr.

비슷한 기술이 constraint11 = cx.sum(x_transports @ train_map.T) `= 2)에 사용돼요, dot 행렬 연산은 기차에 연결된 모든 수송을 추적하고 있어요. 최종 합은 기차에 할당된 모든 컨테이너와 동일하며, 이 값은 2보다 낮거나 같아야 해요.
제약 조건은 두 숫자(“00” 또는 “10”)를 받아요. 이는 특정 주제에 대한 모든 제약 조건을 그룹화하기 위한 것이에요. 이 예시에서 첫 번째 0은 선박과 관련된 모든 제약 조건과 1은 수송과 관련된 모든 제약 조건과 관련된 것이에요. 나중에 제약 조건의 수를 늘리는 필요가 생기면 “0” 뒤에 새로운 숫자를 추가하고 최종 배열을 확장하면 되어요.

최종 솔루션은 다음과 같습니다: x_shippers = [[1, 0], [0, 0], [1, 0], [0, 1] 그리고 x_transport = [[1, 0], [0, 0], [1, 0], [0, 1] (우연히 둘 다 같습니다). 최적화 도구가 두 번째 컨테이너를 라우팅하지 않았습니다. 선박에는 총 3개의 공간만 있기 때문입니다. 첫 번째 컨테이너는 기차를 이용하여 선적자 0으로 이동하고, 세 번째와 마지막 컨테이너는 트럭을 이용하여 선적자 1로 이동합니다.

이제 조금 어려운 도전을 해보겠습니다.

3.3 완전한 예제

이전과 같은 예제를 사용하되 다른 변수를 추가해 보겠습니다: 도크입니다. 이제 공장은 두 개의 가능한 도크로 컨테이너를 운반할 수 있습니다. 기차와 트럭은 각각 비용이 [$50, $70]으로 Dock 0에 도달할 수 있으며, Dock 1은 트럭으로만 비용이 $60으로 도달할 수 있습니다. 두 선적자는 동일한 비용으로 두 도크에 모두 도착할 수 있습니다.

이 문제를 해결하는 방법은 무엇인가요?

아마도 도크 변수를 간단히 더하는 것이 더 어려운 문제를 만드는 것을 깨달을 겁니다. 많은 시도가 도크와 교통을 연결하려 하면 DCPErrors가 발생합니다. 이를 예상대로 모델링하기 위한 전략을 찾아보세요.

…

표태그를 마크다운 형식으로 바꿔보세요.

.... .... .... ....

성공하셨나요? 여기 한 가지 가능한 해결책이 있어요:

대부분 이전 예제와 동일합니다. 그러나 이제 우리는 변수 docks와 transports를 연결하는 AND 변수를 가지고 있다는 점을 주목해주세요.

주요 포인트는 최적화 기능이 x_transport에 대한 값을 선택할 때 x_docks에 대한 선택 옵션에 영향을 미치게 된다는 것입니다. 그러나 독을 선택하는 경우에도 다시 교통에 영향을 줍니다! 이 문제를 해결하기 위해 우리는 AND 변수를 구현하여 최적화 기능이 동시에 결정에 대한 영향을 구별하도록 합니다.

이제 y 변수를 사용하여 구현합니다: y_docks_and_transp = cx.Variable((4, 4), boolean=True, name="docks AND transportations"). 이 변수는 최적화 기능에 의해 업데이트되지만 우리는 이 변수를 두 다른 데이터 소스 사이의 AND 조합으로 강제할 것입니다, 곧 확인하게 될 것입니다. 우리가 사용한 기술은 열에 대한 참조 템플릿을 생성합니다. 즉, 독과 운송을 이 경우에는 결합합니다.

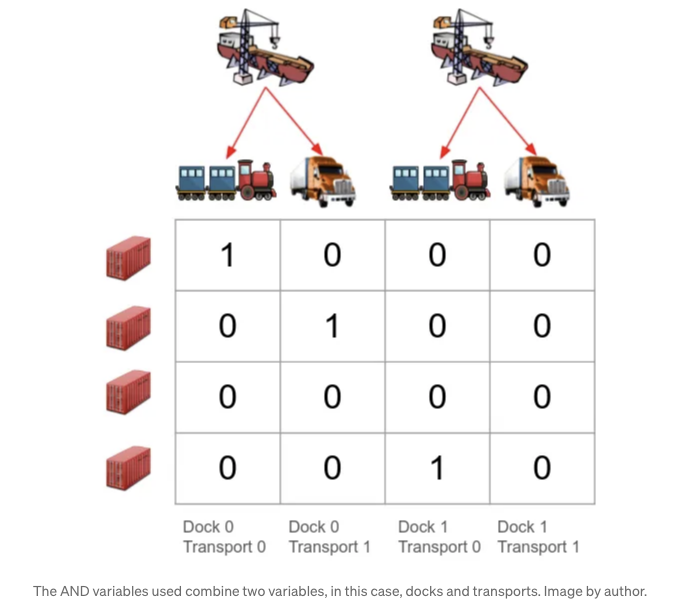
열은 트리 구조입니다. 변수 이름 "y_docks_and_transp"에 "docks"가 먼저 나오는 경우에는 먼저 독이 참조가 되며, 다음에는 운송이 따라옵니다. 위의 예시로 두 번째 행을 살펴보면 두 번째 열에 "1"이라는 값이 있습니다. 이것은 독 0을 선택하고 운송 1(truck)을 선택한다는 것을 의미합니다.

이 템플릿을 사용하면 도크와 운송 변수 모두에 작동하는 다른 데이터 및 제약 조건을 만들 수 있습니다. 예를 들어, 비용을 지정하는 방법은 다음과 같습니다: transport_and_dock_costs = np.array([[50, 70, 0, 60]]), 즉 도크 0과 운송 0(기차)은 50달러 든다는 의미입니다.

최적화 프로그램은 템플릿을 사용하여 각 x 변수를 도크 및 운송 설정으로 전치할 수 있습니다. 이를 위해 다음과 같이 매퍼를 사용했습니다:

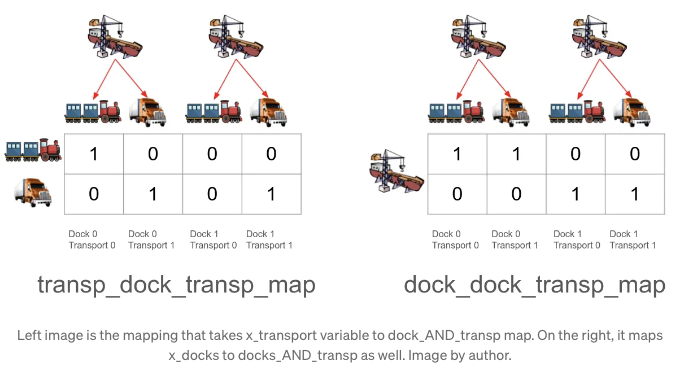
매핑 이미지

최적화 프로그램에서 운송 수단 0을 선택하면, 왼쪽 이미지의 첫 번째 행에 매핑됩니다. 기차가 도크 1을 방문하지 않기 때문에 세 번째 열에 "0"이 있는 것을 기억해주세요. 또한, 변수 이름도 일관된 패턴을 따른다는 것에 주목해주세요: transp_dock_transp_map은 행이 운송수단을 나타내고 도크와 운송수단 사이의 AND 조건에 매핑되는 것을 의미합니다. 여기서 도크가 먼저 나옵니다.

여기서는 y_docks_and_transp를 사용합니다. 최적화 프로그램은 x 변수를 변경할 때 해당 변수를 docks 및 transports 도메인으로 매핑합니다. 그런 다음 두 매핑을 결합하여 정확히 어떤 지점이 도크 및 수송 변수에 해당하는지 확인해야 합니다:

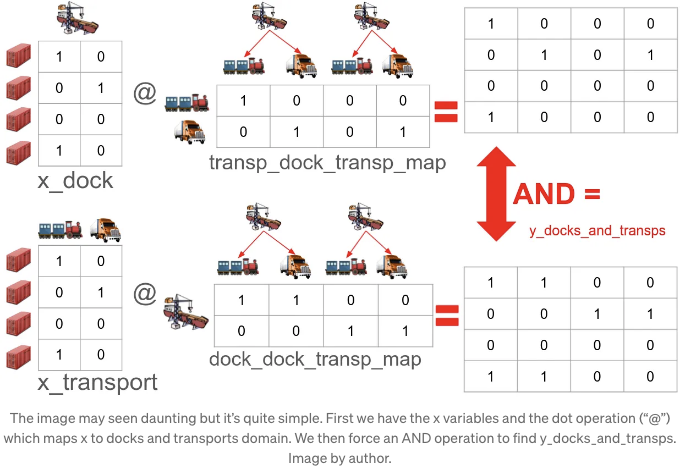
도메인 매핑

위의 이미지에서 보듯이, 먼저 x 변수를 도크 및 수송 도메인으로 전치합니다. 그런 다음 결과를 가져와 AND 연산을 적용하여 각 컨테이너에 대해 구체적으로 어떤 도커와 수송이 선택되었는지 확인합니다:

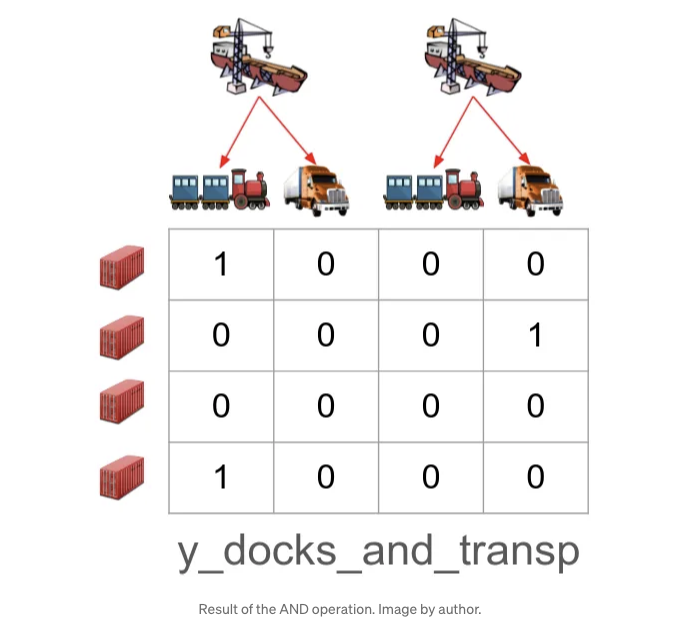
AND 연산

첫 번째 행은 옵티마이저가 Dock 0 및 Train을 선택했음을 의미합니다. 두 번째 행은 Dock 1 및 Truck를 선택했음을 나타냅니다. Dock 1이 기차와 연결되지 않았기 때문에 세 번째 열은 절대 "1"이 되지 않음을 주목하십시오. 이는 유효한 연결의 문제를 해결한 것입니다.

그러나 실제로 이것은 그렇게 간단한 것이 아닙니다. 대부분의 AND 연산 구현 시 DCPError를 유발하는 시도가 많았습니다. 이를 해결하기 위해 우리는 도움이 되는 제약 조건을 사용했습니다:

x1 = x_transports @ transp_dock_transp_map
x2 = x_docks @ dock_dock_transp_map
constraint12 = y_docks_and_transp >= x1 + x2 – 1
constraint13 = y_docks_and_transp <= x1
constraint14 = y_docks_and_transp <= x2
constraint15 = (
    cx.sum(y_docks_and_transp, axis=1) == cx.sum(x_shippers, axis=1)
)

이렇게 함으로써 y_docks_and_transp는 x1과 x2가 모두 "1"인 지점에서만 "1"이 되도록 강제됩니다. 이 기술은 AND 연산이 필요한 경우에 사용할 수 있습니다. constraint15는 라우팅된 컨테이너만 남도록 보장하는 안전 절을 나타냅니다.

여기 x와 y의 최종 값입니다:

x_ships = [[1, 0], [0, 0], [1, 0], [0, 1]]
x_transports = [[1, 0], [0, 0], [1, 0], [0, 1]]
x_docks = [[1, 0], [0, 0], [1, 0], [0, 1]]
y_docks_and_transp = [[1, 0, 0, 0], [0, 0, 0, 0], [1, 0, 0, 0], [0, 0, 0, 1]].

첫 번째 컨테이너는 선적업자에게도킹 0에서 기차로 이동하고, 두 번째 컨테이너는 공장에 남아 있습니다.

모든 예제와 논의된 아이디어를 토대로, 우리는 드디어 회사가 우리에게 제시한 도전에 대해 해결할 수 있게 되었습니다. 지금 즉시 해결해 봅시다!

4. 최종 도전

4.1 입력 데이터

배송업자, 운송 및 그들의 물동량에 대한 정보를 받았습니다:

첫 번째 테이블에서 우리는 공장 0에서 로드(트럭)를 통해 Santos에 위치한 부두로 컨테이너를 운송하는 데 서드 파티 계약을 이용하면 $6000이 든다는 것을 알 수 있습니다. 또한, 선적업자 0은 동 무역을 통해 홍콩으로 컨테이너를 운송할 수 있으며, 컨테이너 당 $8000을 청구할 수 있습니다.

배송업자들의 여유 공간에 대해 이렇게 나타낼 수 있어요:

각 배송업자는 특정 거래에 참여할 수 있고 (따라서 일부 국가들의 그룹), 배에 있는 여유 공간은 매주 변동하며, 1부터 52까지의 숫자로 표시됩니다.

마지막으로, 컨테이너 목록, 제조 공장, 목적지 및 순수 가치:

마지막 열들이 우리가 찾고 있는 최종 결과랍니다. 이 알고리즘의 목표는 일부 제약 조건을 따르면서 운송 업자와 운송을 최소화하는 운송 비용을 찾는 것입니다.

이 포스트에서 사용되지 않을 것이라고 이야기한 것처럼, 각 운송업체와 선적인과 관련된 시간에 대한 또 다른 테이블을 받았습니다.

이 데이터를 나중에 사용할 수 있는 행렬로 변환해야 합니다. 실제로 매우 간단합니다. 배송업체를 예로 들어보죠: 배송업체에 대한 데이터가 포함된 파일을 읽으면서, 새로운 배송업체를 추가할 때마다 더 많은 선박이 추가됨에 따라 증가하는 카운터 값에 각 새로운 배송업체를 연관시킵니다.

우리는 이제 배송업체에 연결된 모든 행렬에 대해서 "0" 인덱스가 나오면 "선적인 0"을 나타낸다는 것을 알고 있습니다. 우리 모델의 모든 구성요소(항구, 운송, 공장)도 마찬가지 아이디어를 따릅니다.

주어진 데이터를 바탕으로 최종 솔루션을 살펴봅시다.

4.2 솔루션

이미 입력 데이터가 준비되었습니다. 이제 직면한 과제는 바로, 비용을 최소화하면서 이 글에서 이미 논의된 제약 조건을 따르면서 각 컨테이너를 라우팅하는 방법은 무엇인가요?

이전 예시에서 제시된 아이디어들은 최종 솔루션이 어떻게 보일지의 전초전이었습니다. 우리가 이 문제를 어떻게 해결했는지 여기에 안내해드릴게요:

함수 optimize는 첫 번째 매개변수인 data_models을 받습니다. 이곳에는 회사에서 입력한 모든 데이터가 처리되어 cvxpy에서 사용할 수 있는 행렬로 변환됩니다. 구체적으로, 데이터 입력 컨테이너는 이전 예제들과 약간 다릅니다:

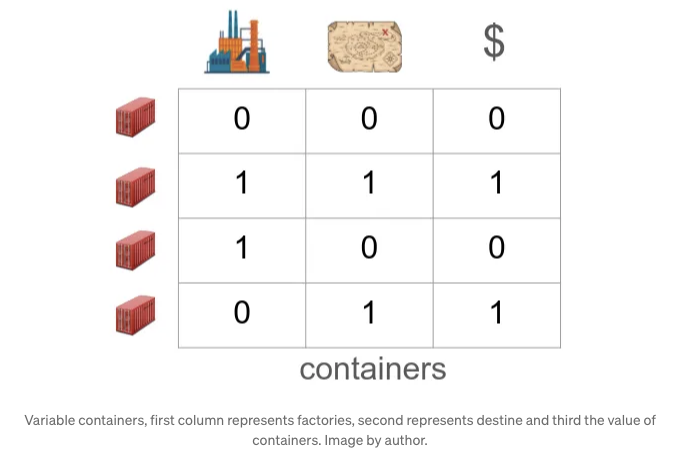
그러나 전반적인 아이디어는 정확히 동일합니다. 고려해야 할 사항은 다음과 같습니다:

72번째 줄에서 코드 shipper_shipper_trade_arr = x_shippers @ shipper_shipper_and_trade_map.matrix는 선적인 선택을 선적인 및 거래 영역으로 변환합니다. 이를 통해 각 거래 및 선적인에 할당된 총 컨테이너를 합산할 수 있습니다.
constr23은 최적화자가 이미 선적인에서 모든 공간을 사용한 경우에만 오버부킹(초과예약)을 강제로 수행하도록 설계되었습니다. 이것은 x_ob_shippers(여기서 "ob"는 오버부킹을 의미)를 선적인 및 거래 영역으로 변환함으로써 수행됩니다.

shipper_ob_trade_indices는 어떤 포인트가 초과 예약되었는지의 매핑 역할을 합니다. 그 정보를 사용하여 constr23를 설치함으로써 해당 포인트에 있는 선적인은 최대 수용량이어야 한다고 명시합니다. 이를 통해 초과 예약이 발생해야 하는 규칙이 모든 보통 공간이 이미 소진되었을 때에만 성립되도록합니다.

제약 조건 3은 이전 예시에서 논의된 AND 기술을 사용합니다. 이를 통해 현재까지 선택된 선적인과 독을 결합하여 이 정보를 사용하여 다른 제약 조건 및 비용을 설치할 수 있습니다.
constr55는 공장과 연결된 독 및 운송에 관한 정보를 결합합니다. 해당 정보를 통해 컨테이너가 위치한 해당 공장에 연결된 독 및 운송을 선택하도록 y_origin_and_transp를 통해 최적화 프로그램에 강요합니다.
비용 함수는 이전 예시에서 논의된 것과 동등합니다.

여기에서 전 세계 컨테이너 분배를 최적화할 수 있는 전체 시스템이 완성되었습니다. 회사에 코드를 전달하기 전에, 의도한 대로 작동하는 것을 보장하기 위해 추가적인 보안층을 추가하고 싶었습니다.

4.3 작동이 잘 되고 있나요?!

코드가 정상 작동하는지 확실히 하기 위해 몇 가지 시나리오를 모방하여 단위 테스트를 구현하기로 결정했습니다. 여기에 예시가 있습니다:

시스템의 백엔드로 Django가 사용되었습니다. 위의 예시에서, 테스트는 최적화 프로그램을 강제로 선박을 과대 예약하도록 하는 입력 데이터를 생성합니다. 그런 다음 결과를 기대값과 비교하여 작동 여부를 확인합니다.

모든 것이 제대로 작동하는 가능성을 높이기 위해 여러 테스트가 구현되었습니다.

5. 결론

이번 도전은 정말 흥미로웠어요. 처음에는 cvxpy 위에 이 솔루션을 구현하는 것이 그다지 간단하지 않았죠. DCPError 오류를 수백 번이나 보았고 문제의 해결책을 찾기까지 시간이 걸렸어요.

결과적으로, 예전에 Excel에서 구현된 Solver와 새롭게 구축된 Solver를 비교하는 것은 심지어 불가능할 수도 있다고 생각해요. 수천 개의 컨테이너로 알고리즘을 테스트해도 전체 처리 시간은 i5 CPU @ 2.20GHz에서 몇 초만에 끝났어요. 게다가, 구현된 솔루션은 현재 솔루션보다 비용 함수와 제약 조건이 더 다양하게 들어가 있었어요.

가능한 단점은 구현이 더 복잡하다는 점이에요 (훨씬 더 많아요) 그리고 새로운 제약 조건을 추가하기 위해 전체 코드를 변경해야 할 수도 있어요. 이는 회사가 희망하는 것만큼 유연하지 않다는 뜻이에요. 그럼에도 불구하고, 장점들을 고려해볼 때, 그것은 만족스러운 교환일 것이었어요.

그럼, 좋은 경험이었죠. 우리만큼 즐기고 배워주셨으면 좋겠네요. 힘들었지만 가치가 있었습니다.

그리고, 항상 다음 미션이 기대될 거예요 ;)!

글로벌 컨테이너 분배 문제 해결을 최적화한 방법