나무는 노드로 구성된 데이터 구조로, 각 노드는 값을 가지고 자식 노드를 가질 수 있는 구조입니다. 나무는 일부 멋진 애플리케이션에서 널리 사용되는 기본적인 데이터 구조입니다.

🌳 중요한 개념:

루트 — 나무의 맨 위 노드 (node1)
부모 노드가 없음
모든 다른 노드는 이를 통해 내려감
노드 — 나무의 기본 단위 (모든 노드 1→12)
가장자리 — 두 노드 사이의 링크
내부 노드 — 적어도 하나의 자식을 가진 노드(노드 2, 3, 4, 6, 7)
잎 — 자식이 없는 노드(노드 5, 8, 9, 10, 11, 12)

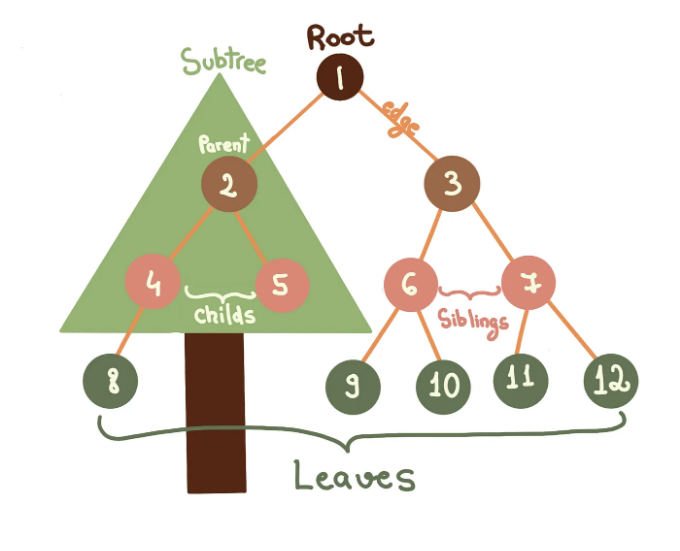
부모 및 자식 관계
- 자식(child): 다른 노드에서 내려온 노드(예: 노드 4, 5)
- 부모(parent): 하나 이상의 자식 노드를 가진 노드(예: 노드 2)
- 형제(siblings): 동일한 부모 아래 동일한 계층 수준의 노드(예: 노드 6, 7)
서브트리(subtree): 해당 노드와 하위 노드를 모두 포함하는 트리 내의 모든 노드(예: 노드 2, 4, 5)
레벨, 높이 및 깊이
- 깊이(depth): 루트부터 해당 노드까지의 엣지 수(예: 노드 7 → 깊이 2 → 엣지 1→3→7)
- 높이(height): 해당 노드부터 가장 긴 리프까지의 엣지 수(예: 노드 1 → 높이 3 → 엣지 1→3→7→11)
- 레벨(level): 계층적 깊이에 따른 노드의 위치(예: 시각화할 때 동일한 레벨의 모든 노드는 동일한 행에 있음) (예: 노드 4, 5, 6, 7 → 레벨 2)

이진 트리(Binary Trees):

이진 트리는 각 노드가 최대 두 개의 자식을 가지는 특별한 종류의 트리입니다. 이 자식들은 종종 오른쪽 자식과 왼쪽 자식으로 참조됩니다.

이진 트리의 종류:

Full binary tree:
- 각 노드는 2개의 자식 노드를 갖거나 자식 노드가 없어야 함
Complete binary tree:
- 모든 레벨이 완전히 채워져 있으나 마지막 레벨은 왼쪽부터 오른쪽으로 채워질 수 있음

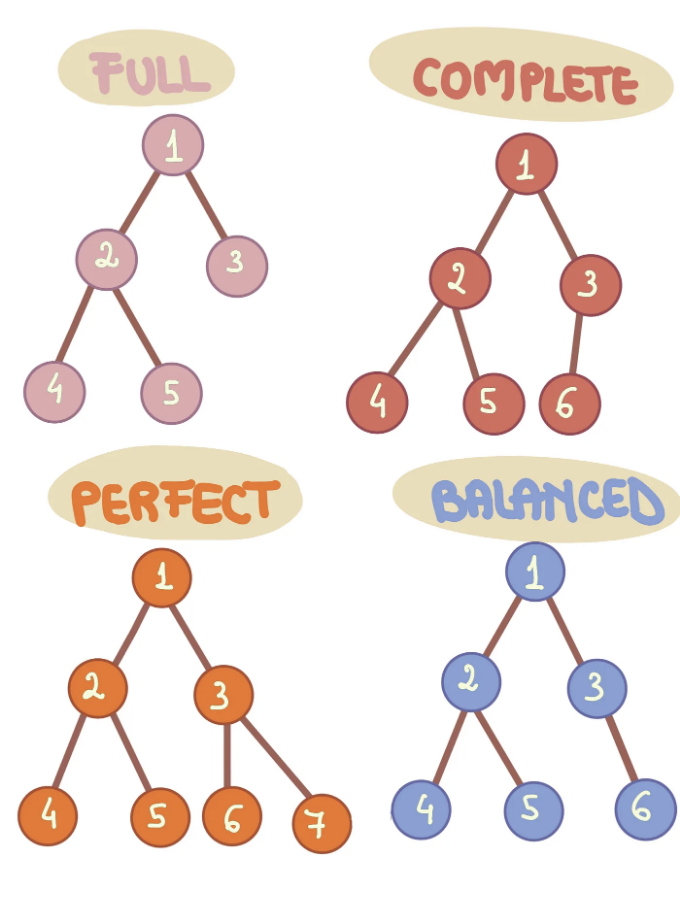
Binary Tree Image

Perfect binary tree:
- 모든 리프 노드가 동일한 레벨에 있는 완전한 이진 트리
Balanced binary tree:
- 모든 노드의 왼쪽과 오른쪽 서브트리 사이의 높이 차이가 최대 1인 이진 트리

Binary Tree에서 주요 작업 🌳:

트리에서 모든 노드를 체계적인 방법으로 방문하는 것을 순회(traversal)라고 합니다.

               1
            /     \
 
         2           3
       /   \       /    \
      4     5      6     7
    /  \   / \    / \    / \
   8    9 10 11  12 13  14 15

중위 순회 (왼쪽, 루트, 오른쪽): 왼쪽 서브트리, 루트, 그리고 오른쪽 서브트리를 순서대로 방문합니다 8→4→9→2→10→5→11→1→12→6→13→3→14→7→15
전위 순회 (루트, 왼쪽, 오른쪽): 루트, 왼쪽 서브트리, 그리고 오른쪽 서브트리를 순서대로 방문합니다 1→2→4→8→9→5→10→11→3→6→12→13→7→14→15
후위 순회 (왼쪽, 오른쪽, 루트): 왼쪽 서브트리, 오른쪽 서브트리, 그리고 루트 순서로 방문합니다 8→9→4→10→11→5→2→12→13→6→14→15→7→3→1
레벨 순회 (너비 우선): 상위에서 하위로 레벨별로 방문합니다 1→2→3→4→5→6→7→8→9→10→11→12→13→14→15

코드 조각:

° 클래스 정의:

class TreeNode {
    value: number;
    left: TreeNode | null;
    right: TreeNode | null;

    constructor(value: number, left: TreeNode | null = null, right: TreeNode | null = null) {
        this.value = value;
        this.left = left;
        this.right = right;
    }
}

° 순회 — 중위 순회:

function traverse(node: TreeNode | null): number[] {
    let list: number[] = [];
    if(node){
        // 중위 순회
        // 이 부분의 코드는 다른 유형의 순회로 대체할 수 있습니다
        list.push(...traverse(node.left));
        list.push(node.value);
        list.push(...traverse(node.right));
    }
    return list;
}

° 테스트:

let left = new TreeNode(2, new TreeNode(4), new TreeNode(5));
let right = new TreeNode(3, null, new TreeNode(6));
let root = new TreeNode(1,left, right);
console.log(traverse(root));

° 출력: [4,2,5,1,3,6]

° 순회 — 전위 순회 — 위와 동일하며, 아래 내용을 스왑하시면 됩니다:

list.push(node.value);
list.push(...traverse(node.left));
list.push(...traverse(node.right));

° 출력: [1,2,4,5,3,6]

° 순회— 후위 순회 — 같은 것이지만, 다음을 바꾸기만 합니다:

list.push(...traverse(node.left));
list.push(...traverse(node.right));
list.push(node.value);

° 결과: [4,5,2,6,3,1]

왜 이진 🌳?

이진 트리는 프로그래밍에서 또 다른 개념으로 보일 수 있지만, 이제까지 아마 알겠지만, 많은 강력한 애플리케이션의 기초입니다. 검색을 최적화하거나 데이터를 더 효율적으로 구성하는 것에서부터, 이 데이터 구조는 복잡성을 쉽게 탐색할 수 있도록 도와줄 수 있습니다.

이진 트리란 시각적 가이드

이진 트리(Binary Trees):

이진 트리의 종류:

Binary Tree에서 주요 작업 🌳:

코드 조각:

왜 이진 🌳?