개요
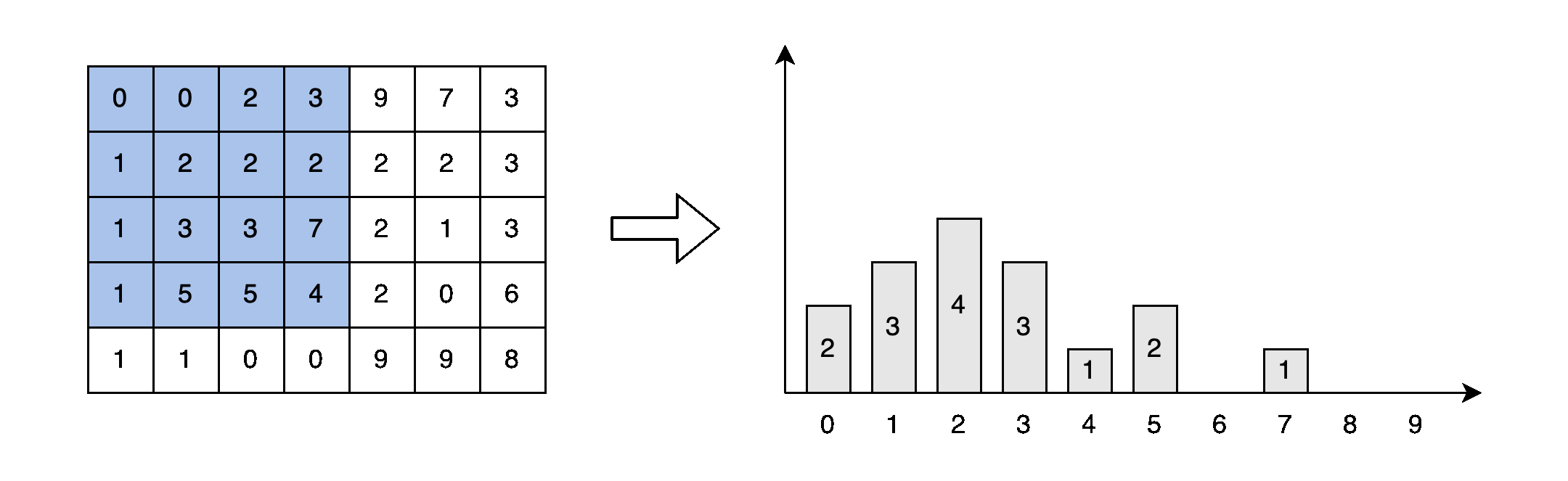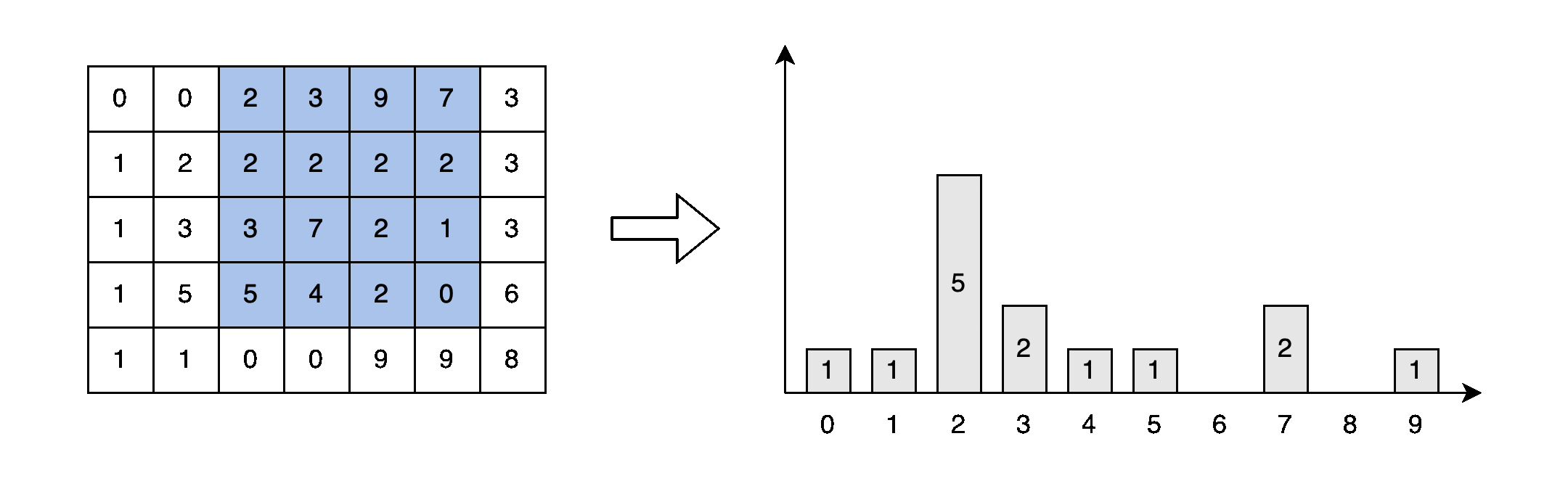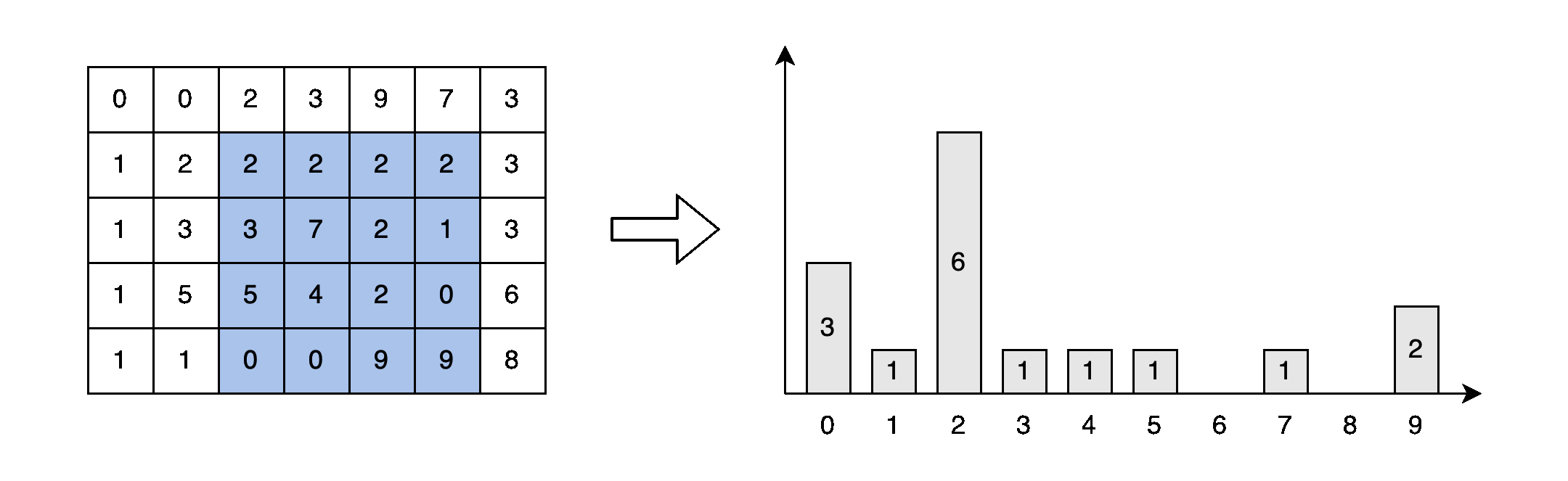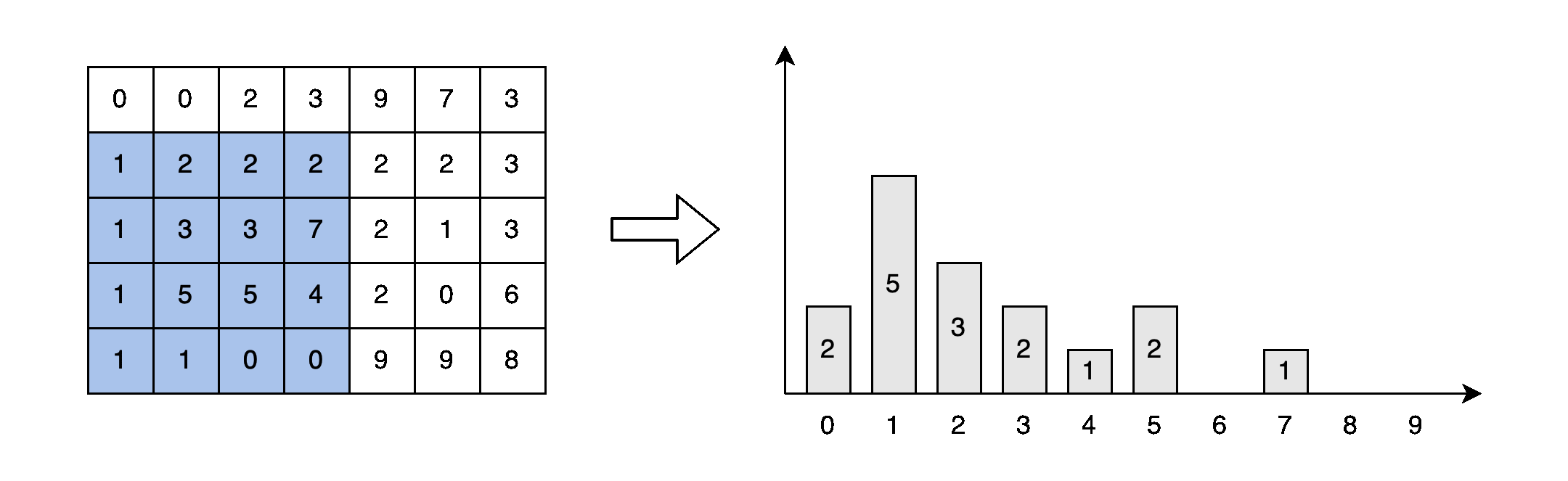
중앙값 필터는 신호 및 이미지 처리에서 데이터를 부드럽게 하는 데 필요한 기본 작업 중 하나입니다. 중앙값 필터의 개념은 간단하지만, 지난 20년 동안 해당 분야에서 더 효율적으로 만들기 위해 다양한 알고리즘이 제안되었습니다.
본 글에서는 논문 "A fast two-dimensional median filtering algorithm"에서 제안된 히스토그램 기반의 효율적인 중앙값 필터 알고리즘을 살펴보겠습니다¹. 이 알고리즘은 다양한 프로그래밍 언어로 작성된 많은 이미지 처리 라이브러리에 널리 구현되어 있습니다. 우리는 이를 파이썬으로 구현한 것을 통해 이해하기 쉽도록 설명하겠습니다.
만약 코딩 면접을 준비하고 있거나 이미지 처리 전문가로 히스토그램이 중앙 필터 구현에 어떻게 도움이 될 수 있는지 궁금한 경우, 아래 섹션을 함께 살펴보시기 바랍니다.
문제 설명: 2D 중앙 필터
중앙값(median)에 대한 정의부터 시작해 보겠습니다. 중앙값은 순서대로 정렬된 목록에서 중간 값입니다. 이는 두 가지 경우로 나뉠 수 있습니다.
- 리스트의 크기가 짝수인 경우: 중앙값은 두 중간 값의 평균입니다. 예를 들어, 리스트 [1, 8, 9, 11]의 중앙값은 (8+9)/2 = 8.5입니다.
- 리스트의 크기가 홀수인 경우: 중앙값은 중간 값입니다. 예를 들어, 리스트 [7, 8, 9, 10, 17]의 중앙값은 9입니다.
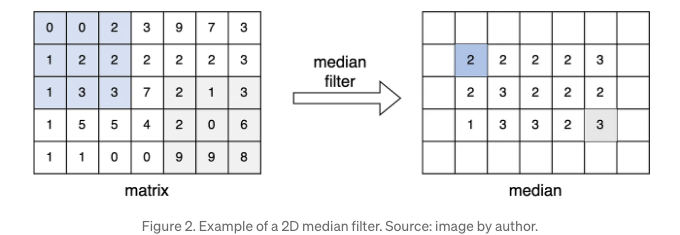
2D 중앙값 필터는 이차원 행렬에서 하위 영역의 중앙값을 추출합니다. 형식적으로, 2D 배열 행렬과 윈도우 크기 k가 주어지면 중앙값 필터는 각 픽셀이 해당 행렬 하위 영역의 중앙값인 필터링된 이미지를 반환합니다. 5x7 행렬과 해당 중앙값의 예시가 도 2에 제공되어 있습니다.
이 글에서는 일반적인 패턴에 집중하고 코드 간결성을 유지하기 위해 경계 요소를 건너뛸 것입니다. 이 글에서 무시된 경계 요소는 빈 셀로 표시됩니다.
알고리즘
해결책 1: 정렬
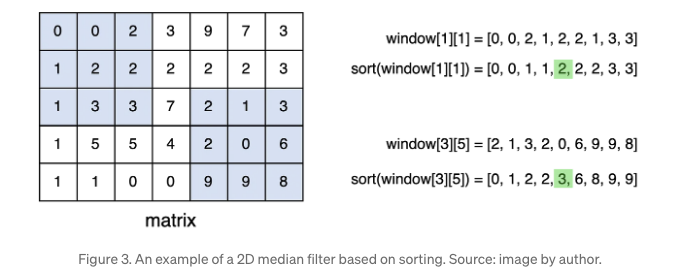
가장 직관적인 방식으로 시작해보겠습니다. 창은 2D 행렬을 가로지르는데, 언제든지 창 내의 요소는 정렬되어 있고, 중심에 있는 요소가 중앙값으로 선택됩니다. 예를 들어, 창이 (5, 3) 위치에 중심이 있을 때, 창[3][5] 내의 정렬된 픽셀은 [0, 1, 2, 2, 3, 6, 8, 9, 9]입니다. 중앙값은 값이 3인 5번째 요소입니다.
시간 복잡도: O(m • n • k²log k²)
창에 있는 요소의 수는 k * k입니다. 최상의 정렬 알고리즘은 요소를 오름차순 또는 내림차순으로 변환하는 데 O(k²log k²)의 시간이 소요됩니다. 정렬은 전체 이미지에서 m * n번 적용됩니다. 전체 시간 복잡도는 O(m • n • k²log k²)입니다.
공간 복잡도: k²
정렬된 픽셀을 저장하기 위해 크기가 k²인 추가 배열이 사용됩니다.
구현
아래는 정렬 기반 솔루션의 구현입니다. 창의 이동은 바깥쪽 루프에서 매개변수 y와 x로 관리됩니다. 내부 루프에서는 창 내의 요소가 수집되어 정렬됩니다. 창 중앙의 요소가 중앙값으로 선택되어 새 행렬인 filtered의 해당 위치에 저장됩니다.
def median_sort(matrix: List[List[int]], k: int):
m, n = len(matrix), len(matrix[0])
filtered = [[0] * n for i in range(m)]
win_size = k * k
for y in range(k//2, m-k//2):
for x in range(k//2, n-k//2):
win = []
for yy in range(-k//2+1, k//2+1):
for xx in range(-k//2+1, k//2+1):
win.append(matrix[y+yy][x+xx])
win.sort()
if win_size % 2 == 0:
mdn = (win[win_size//2] + win[(win_size-1)//2])//2
else:
mdn = win[win_size//2]
filtered[y][x] = mdn
return filtered
솔루션 2: 러닝 히스토그램
히스토그램 기반 접근법을 살펴보기 전에, 첫 번째 접근법을 되짚어보고 그 계산에 대해 조사해 봅시다. 먼저, 알고리즘은 언제든지 정렬을 필요로 하므로 전체 처리 시간이 행렬 크기와 함께 증가합니다. 행렬/커널이 더 크거나 작을수록 더 많은 정렬이 필요합니다.
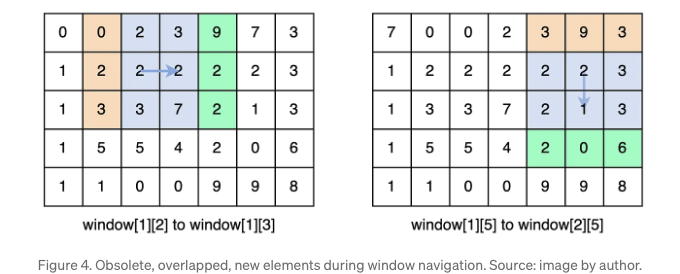
게다가, 아마도 이미 알고 계실 것이지만, 창이 이동할 때 대부분의 픽셀은 반복적으로 정렬됩니다. 그림 4에서 파란색으로 표시된 여섯 요소는 window[1][2]와 window[1][3]에서 두 번 정렬됩니다. 중복 정렬 없이 겹치는 요소의 순서를 유지하는 방법이 없을까요?
각 창 탐색 시, 창에는 새로운 요소가 포함되고 오래된 요소가 제거됩니다. 오래된 요소와 새로운 요소는 그림 4에서 빨간색과 녹색 요소로 표시됩니다. 예를 들어 창이 (5,1)에서 (5,2)로 이동할 때 [2, 0, 6] 요소가 창에 추가되고 [3, 9, 3] 요소가 제거됩니다.
중복되는 요소의 순서를 유지하고 새로운 요소와 오래된 요소에만 작용하는 방법이 있는지 알고 계십니까?
런닝 히스토그램
다음으로, 러닝 히스토그램을 기반으로 하는 기본적인 방법에 대해 살펴보겠습니다. 히스토그램은 데이터 분포에 대한 통계 도구입니다. 중앙값에 접근하기 위한 훌륭한 방법으로, 왜냐하면 다음 두 가지 이유 때문입니다:
- 히스토그램은 빈도에 대응하는 값을 정렬된 방식으로 갖고 있습니다.
- 요소를 추가하거나 제거하기 위해서는 히스토그램에서 해당 요소를 찾은 후 연관된 빈도를 1씩 증가 또는 감소시킬 수 있습니다. 히스토그램은 인덱스가 요소의 값인 방식으로 설계될 수 있습니다. 요소에 접근하기 위해 O(1) 시간에 인덱싱할 수 있습니다. 빈도의 증가 또는 감소는 또 다른 O(1) 시간이 소요됩니다. 이러한 작업들은 총 O(1) 시간 복잡도를 가집니다.
러닝 히스토그램은 언제든지 윈도우 안의 요소들의 분포를 보여주는 지속적으로 업데이트된 히스토그램을 유지하는 것을 참조합니다. 러닝 히스토그램의 예시는 본문 상단의 특집 이미지에서 보여집니다.
단계 1: 요소 추가/제거
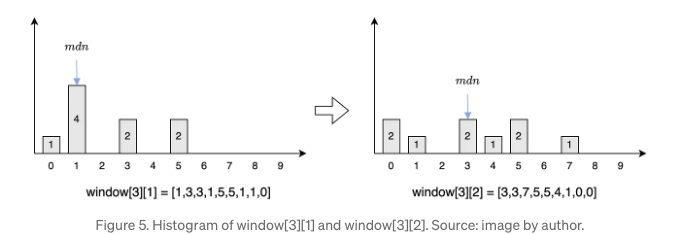
이 테스크에서 히스토그램이 얼마나 중요한 역할을 하는지 알아보기 위해 예시로 들어가 봅시다. 윈도우[3][1]과 윈도우[3][2]의 히스토그램이 그림 5에 제공되어 있습니다. 새로운 요소 7, 4, 0이 빈도수를 1 증가시켜 윈도우에 추가되었습니다. 반면, 구식 요소 1, 1, 1은 빈도수를 1 감소시켜 제거되었습니다. 두 작업은 O(1) 시간이 걸리며 이로 인해 히스토그램 업데이트가 매우 효율적으로 이루어집니다.
아래에 구현된 코드가 제공되었습니다. get_strip() 함수는 각 위치에서 이전 요소와 새로운 요소를 반환합니다. 두 개의 루프가 각 선택된 요소를 순환하며 히스토그램을 업데이트합니다.
def get_strip(indices, i, k):
y, x = indices[i]
prev_y, prev_x = indices[i-1]
dir_y, dir_x = y - prev_y, x - prev_x
offset = k // 2
if dir_y == 0:
old = [(yy, x - dir_x * (offset+1)) for yy in range(y - offset, y + offset + 1)]
new = [(yy, x + dir_x * offset) for yy in range(y - offset, y + offset + 1)]
else:
old = [(y - dir_y * (offset+1), xx) for xx in range(x - offset, x + offset + 1)]
new = [(y + dir_y * offset, xx) for xx in range(x - offset, x + offset + 1)]
return old, new
for i in range(1, len(indices)):
y, x = indices[i]
olds, news = get_strip(indices, i, k)
for yy, xx in olds:
histogram[matrix[yy][xx]] -= 1
if matrix[yy][xx] < mdn:
ltmdn -= 1
for yy, xx in news:
histogram[matrix[yy][xx]] += 1
if matrix[yy][xx] < mdn:
ltmdn += 1
Step 2. Identify the median in the histogram
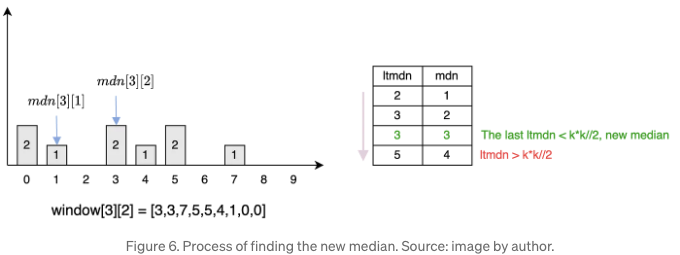
이 작업에서 히스토그램을 사용하는 도전 과제는 히스토그램에서 중앙값을 식별하는 방법입니다. 원본 논문에서 중앙값보다 작은 요소의 수를 기록하는 변수 ltmdn을 사용했습니다. 다른 상수 변수 th = k²/2는 ltmdn의 기대값을 나타냅니다. 예를 들어, 커널 크기가 5인 경우, 창에는 5²=25개의 요소가 포함되며 중앙값보다 작은 요소의 수는 5²/2 = 12개입니다.
ltmdn과 th의 차이의 부호는 중앙값의 이동 방향을 나타냅니다.
- ltmdn[t] ` th: 현재 중앙값 mdn[t]이 이전 중앙값 mdn[t-1]보다 큽니다. 여기서 매개변수 t는 탐색 경로를 따라 중앙값의 순서를 나타냅니다.
- ltmdn[t] ` th: 현재 중앙값 mdn[t]이 이전 중앙값 mdn[t-1]보다 작습니다.
새로운 중앙값 mdn[t]를 찾기 위해 이전 중앙값 mdn[t-1]을 업데이트하고 ltmdn[t]이 th를 만날 때까지 계속됩니다. 이것은 루프 내에서 선형 시간 내에 수행할 수 있습니다. 반복을 중단하는 요소가 새로운 중앙값입니다.
아래 예시는 Figure 6에 나와 있습니다. 이전 중간값 mdn[t-1] = 1이며 ltmdn[t]=2입니다. 마지막으로 ltmdn[t] = 3보다 작은 값을 찾을 때까지 중간값이 1씩 증가합니다.
해당 코드 스니펫은 아래와 같습니다.
if ltmdn > th: # 현재 창에 있는 중간값이 이전 창에 있는 것보다 작음
while ltmdn > th:
mdn -= 1
ltmdn -= histogram[mdn]
else:
while ltmdn + histogram[mdn] <= th:
ltmdn += histogram[mdn]
mdn += 1
시간 복잡도: O(m • n • (2k +h))
알고리즘은 히스토그램을 업데이트하고 새 중간값을 찾는 단계를 포함합니다. 그 기준은 이전 중간값보다 작은 픽셀의 개수에 따라 설정됩니다. 빈도를 수정하여 히스토그램을 업데이트하는 데 O((k+k) • 1) 시간이 소요됩니다. 요소가 h개의 유효한 값을 가진다고 가정하면, 중간값을 이동하는 데 O(h) 시간이 걸립니다. 창은 m * n 단계로 전체 이미지를 순회합니다.
공간 복잡도: h
필요한 추가 공간은 h개의 구획을 가진 히스토그램입니다. 매개변수 h는 요소의 값 수를 나타냅니다. 예를 들어, 요소 값이 256으로 설정되어 있고, 0부터 255까지의 픽셀을 가진 8비트 이미지의 중간값을 계산하는 경우에는 h가 256으로 설정됩니다.
구현
아래에 파이썬에서의 완전한 구현이 제공되었습니다. 이는 주로 논문의 의사코드를 따라가지만, 지그재그 패턴으로 대안적으로 창을 탐색합니다.
def median_hist(matrix: List[List[int]], k: int):
m, n = len(matrix), len(matrix[0])
filtered = [[0] * n for i in range(m)]
win = []
h = 256 # bins의 개수
histogram = [0] * h
for y in range(k):
for x in range(k):
win.append(matrix[y][x])
histogram[matrix[y][x]] += 1
win.sort()
th = k * k // 2
mdn = win[th] # 창 내의 중앙값
ltmdn = 0 # 창 내에서 mdn보다 작은 회색 레벨을 갖는 픽셀 수
for y in range(k):
for x in range(k):
if matrix[y][x] < mdn:
ltmdn += 1
filtered[k//2][k//2] = mdn
indices = get_zigzag(m, n, k)
for i in range(1, len(indices)):
y, x = indices[i]
olds, news = get_strip(indices, i, k)
for yy, xx in olds:
histogram[matrix[yy][xx]] -= 1
if matrix[yy][xx] < mdn:
ltmdn -= 1
for yy, xx in news:
histogram[matrix[yy][xx]] += 1
if matrix[yy][xx] < mdn:
ltmdn += 1
if ltmdn > th: # 현재 창의 중속값이 이전 창의 것보다 작음
while ltmdn > th:
mdn -= 1
ltmdn -= histogram[mdn]
else:
while ltmdn + histogram[mdn] <= th:
ltmdn += histogram[mdn]
mdn += 1
filtered[y][x] = mdn
return filtered
창 탐색
위 섹션에서 두 알고리즘의 개념과 주요 흐름을 살펴보았습니다. 마지막으로 행렬을 따라 이동하는 창에 대해 고려해 봅니다.
행/열-우선
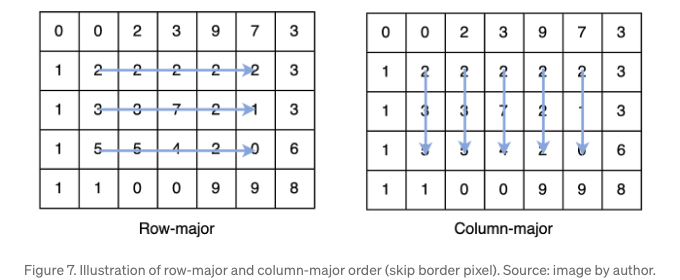
정렬 기반 방식에서 중앙값 계산은 서로 독립적입니다. 예를 들어, window[2][3]와 window[2][4]에서의 중앙값 계산은 서로 정보를 공유하지 않고 별도로 수행됩니다. 창 이동은 행-우선 또는 열-우선과 같은 임의의 순서를 따를 수 있습니다. Figure 7에서 보여지듯이.
지그재그 순회
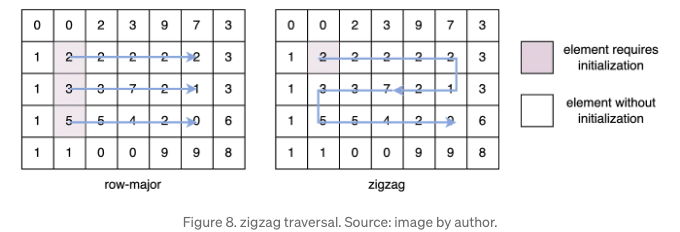
반면에 히스토그램 기반 방법은 (1, 1)에 대한 초기화를 제외하고 이전 정보에 의존합니다. 행 주요 또는 열 주요 반복은 각 행 또는 열의 시작 부분에서 다중 초기화가 필요하며 O(m•k²logk²) 또는 O(n•k²logk²) 시간이 소요됩니다.
윈도우는 지그재그 순서로 행렬을 검토하며 단 하나의 초기화만 필요합니다. Figure 8에서 초기화가 필요한 요소들은 회색 셀로 표시되어 있습니다. 행 주요 순서는 세 번의 초기화가 필요하지만, 지그재그는 단 한 번만 필요합니다. 지그재그 순회는 행렬 크기가 큰 경우 특히 무거운 정렬 작업의 수를 크게 줄입니다.
아래는 지그재그 순회를 따라 좌표를 수집하는 스크립트입니다.
def get_zigzag(n_row, n_col, k):
indices = []
offset = k // 2
for i in range(offset, n_row-offset):
coordinates = [[i, j] for j in range(offset, n_col-offset)]
if i % 2 == 0:
coordinates = coordinates[::-1]
indices += coordinates
return indices
성능
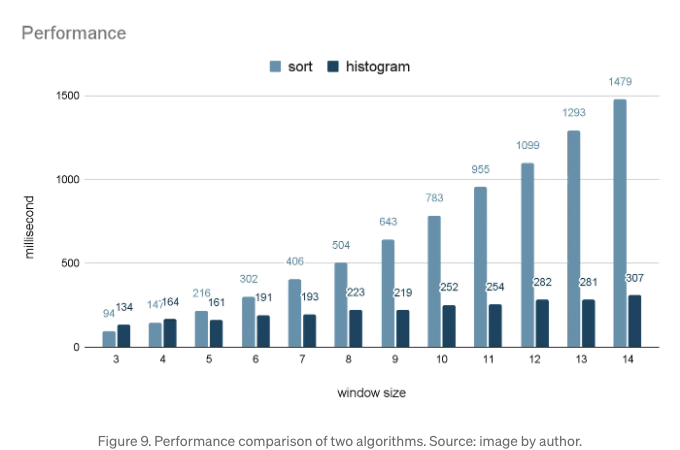
두 가지 접근 방식을 살펴본 후 히스토그램 기반의 접근 방식이 이론적으로 더 효율적임을 알게 되었으니, 서로 다른 규모에서 성능을 비교해 보겠습니다.
요약
256 x 256 매트릭스에서 3에서 14까지 다른 창 크기에서 성능을 비교한 Figure 9를 살펴보겠습니다. 창 크기가 커질수록, 정렬 기반 알고리즘의 계산 시간이 크게 증가하는 반면, 히스토그램 기반 접근 방식은 더 일관되게 유지됩니다. 두 알고리즘의 비율은 창 크기 3에서 0.7014(=94/134)에서 창 크기 14에서 4.8175(=1479/307)로 증가합니다. 히스토그램 기반은 특히 창 크기가 커질수록 훨씬 효율적입니다.
256 x 256 매트릭스에서 x축에 표시된 다양한 창 크기에서 수행 성능을 비교하는 그림 9를 확인했습니다. 창 크기가 증가함에 따라 기준 정렬 알고리즘의 계산 시간은 상당히 증가하는 반면 히스토그램 기반 방식은 상대적으로 일관성이 있습니다. 두 알고리즘의 비율은 0.7014(창 크기 = 3에서 94/134)에서 4.8175(창 크기 = 14에서 1479/307)로 증가합니다. 히스토그램 기반 방법은 특히 창 크기가 커질수록 훨씬 더 효율적입니다.
참고
[1] T. Huang, G. Yang and G. Tang, "A fast two-dimensional median filtering algorithm," in IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 27, no. 1, pp. 13-18, February 1979