내가 너를 흥분시키는 농담이 있어:

당연히 농담을 설명할 필요는 없지만, 좋은 수학자들처럼 조금만 과대해석해보자면, 입자의 정보가 그룹의 다른 모든 입자에게 전달될 수 있다는 것을 묘사한 농담이 있어. 이 개념은 내가 방금 한 농담보다 훨씬 깊고 더 발전시킬 수 있는 가능성이 있어.

새 떼나 물고기 떼와 같은 자기 조직화된 시스템을 고려해보자. 우리는 이 시스템을 입자로 구성되었다고 정의할 수 있어 (예를 들어, 한 입자는 새이다). 또한 이러한 입자들이 공간에서 움직이며 자신의 위치를 두 가지 요인에 기반하여 조절한다고 가정할 수 있어:

• 특정 입자가 알고 있는 최상의 위치: 새들이 스스로에게 최선으로 생각하는 위치.
• 모든 입자들끼리 “소통”하여 주는 전역 최상의 위치: "주요 새"에서 지시 받는 일을 하는 새들이야.

자연에서 "최고"는 무엇인가요? 새를 위해 최선인 일은 무엇인가요? "떼"에게 가장 좋은 것은 무엇일까요? 이에 대해 제게 물어보셔서 정말 죄송하지만, 정말 감을 잡을 수 없어요. 알고 있는 것은 자연의 이러한 행동을 관찰함으로써 매우 매력적인 최적화 알고리즘을 형식화할 수 있다는 점입니다. 다시 말해, 최상이 무엇인지 정의하면 선택한 함수를 최적화하기 위해 이 진화적 접근법을 사용할 수 있습니다.

이 알고리즘을 먼저 소개하겠습니다. 이것은 Particle Swarm Optimization (PSO) 알고리즘입니다. 알아요, 이건 정말 큰 도약이죠. "최적화"가 무엇인가요? 왜 갑자기 수학 얘기를 하고 있죠? 무엇을 최적화하고 있는 거죠? 이 글을 통해 이 모든 단계에 대해 다루고, 더 중요한 것은 Python을 사용하여 우리만의 ParticleSwarmOptimizer() 클래스를 만들기 위해 객체 기반 프로그래밍을 사용할 거에요. 다시 말해, 이론부터 실제까지 PSO 세계를 다룰 거에요.

시작해 봅시다! 🐦🐦🐦

0. "최적화" 소개하기

"만약 'Particle Swarm Optimization'에 대해 읽고 있다면 이미 '최적화'에 대해 조금 알고 있을 가능성이 높고 'particle swarm'에 대해 잘 모를 것이라고 생각하기 때문에 이에 대해 너무 많은 시간을 들이지 않고 독자들을 지루하게 만들고 싶지 않아요.

그러나 문제에 대해 약간의 형식화를 제시하고 싶어해요. 앞서 말한 대로 수학적으로, '떼에게 최선의 일은 무엇인가요?'

수학적으로 말하자면, '떼의 새들' (또는 'particles')은 K-차원 공간에 있는 점들입니다. 실제 공간이라면, 'domain'이 우리가 사는 3D 공간이 될 수 있지만 그것보다 훨씬 큰 경우도 있습니다. 사실, 이 방법은 '새' 예시를 잊고 우리는 주어진 함수의 최솟값이나 최댓값을 찾기 위해 이 방법을 일반적으로 사용할 수 있다는 점을 고려할 때 흥미로워집니다.

예를 들어, 집값이 알고리즘에 의해 자동 생성된다고 가정해봅시다 (사람이 개입하지 않는 것은 매우 위험하지만 어쨌든):"

이제 이건 그다지 의미가 없어보입니다, 맞죠? "집" 아이콘이 무엇인가요? 우리는 기능 목록을 가질 것입니다. 예를 들어 위치, 크기 등...

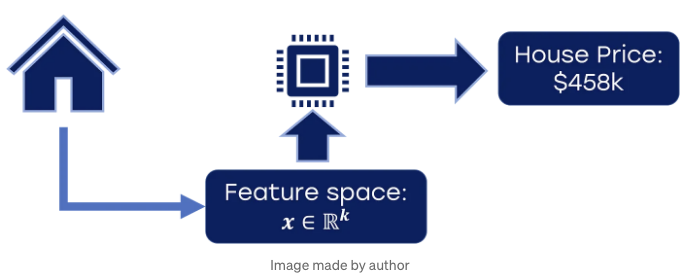
이제 이야기가 맞죠. 집은 기능 공간으로 변환되었습니다. 그래서 각 집은 k 차원 점입니다. 기능 공간을 집 가격으로 변환하는 "흑색 상자" 함수입니다:

아래가 게임의 본질이에요:

이게 우리의 최적화 문제야.

PSO의 최종 목표는 x_min의 좌표를 찾는 것입니다. 이를 어떻게 다루는지 살펴봅시다.

1. 입자군 최적화(Particle Swarm Optimization) 소개

자, 그럼 이 아이디어는 무엇일까요? 말했듯이, 이 아이디어는 서로 정보를 교환하여 전역 최솟값을 찾기 위해 협력하는 입자군을 만든다는 것입니다. 만일 원하신다면, 이는 “Stranger Things”와 같은 TV 프로그램에서 발생하는 일과 매우 유사합니다. 거기에 이겨야 할 적이 있고 모든 캐릭터가 서로 협력하여 가능한 모든 방법을 사용해 대화하는 것과 유사합니다.

좀 더 기술적으로, 우리는 num_particles(입자 수)개의 입자로 시작합니다. 이들 입자는 무작위 위치를 가지며, 각 위치마다 비용 함수 L이 그 값을 갖게 됩니다. 예를 들어, 입자 1은 위치 x_1과 비용 L(x_1)을 갖게 됩니다. 이것이 반복 0이며, 이 첫 번째 반복 이후에 시스템을 구축했습니다. 이제 시스템이 발전해야 합니다. 어떻게 이를 할까요? "속도"라고 불리는 양을 통해 이를 수행합니다. 특정 입자 x에 대해, 각 차원 (i) 및 각 반복 (j)에 대해 다음을 갖습니다:

아래는 더 우아한 벡터 형태입니다:

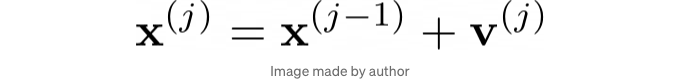
이제 v를 어떻게 정의해야 할까요? 여기서 이 방법의 아름다움이 드러납니다. 벡터 v는 기본적으로 세 가지 구성요소가 있습니다:

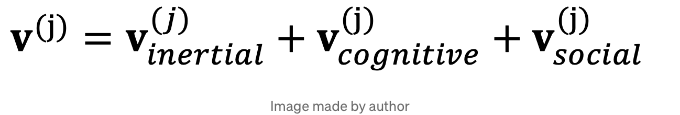
Let’s explore them:

• v_intertial is basically the memory of the previous velocity. The term comes from physics where the inertial system is a system of reference where a body will remain at rest or move at a constant velocity.

where k_intertial is a constant.

• v_cognitive is the velocity that is suggested by the own particle (that is in some way cognitive). It suggests that we should move in the direction where we know we have our best for that particle. We also add a little bit of randomness r_1 (random number):

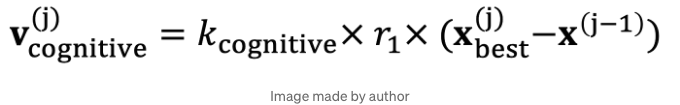
k_cognitive is again a constant. x_best is the best (lowest cost function) for the x particle.

• v_social은 모든 다른 입자로부터 정보를 수집합니다. 우리는 모든 입자에게 가장 좋은 방향으로 이동합니다.

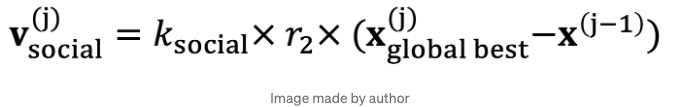
k_social은 상수이며, r_2는 무작위 값이며, x_'global best'는 모든 입자에 대한 최상의(최소 비용 함수)입니다.

지금, 내 생각에는, 매우 우아하다고 생각합니다. 여기서 끝내겠습니다:

• 특정 개수의 무작위 입자(즉, 무작위 위치의 입자)를 선택하여 시작합니다.
• 속도 매개변수에 기반하여 이러한 입자들을 이동시킵니다.
• 이러한 속도는 세 가지 요소에 의해 결정됩니다: 관성은 이전 속도를 유지하며, 인지 속도는 입자에게 가장 적합한 방향으로 계속 이동하게 하고, 사회적 속도는 전체 입자 그룹이 제안하는 방향으로 계속 이동하게 합니다.
• 우리는 각 반복마다 이러한 입자의 위치를 변경하며, num_iteration에 도달할 때까지 반복합니다. 그런 다음 최적의 옵션을 선택합니다.

오늘은 여기까지! 이제 파이썬 코드를 실행해 보겠습니다 :)

2. PSO 구현

우리는 PSO를 구축하기 위해 두 개의 클래스를 사용할 것입니다. 첫 번째 클래스는 단일 입자 클래스이며, 두 번째 클래스는 단일 입자 클래스를 빌더로 이용하여 우리의 떼를 구축합니다.

우선 구축하고 싶은 첫 번째 항목은 constants.py 파일입니다. 이 파일은 입자의 경계, 반복 횟수, 그리고 모든 k 값 등의 기본 정보를 모두 보관합니다. 이 정보를 어떻게 바꿔야 하느냐고요? .json 파일을 만들어서 "config/pso_config.json"이라는 이름으로 넣으면 됩니다. 파일이 없으면 제가 제공하는 스크립트에 의해 파일이 생성됩니다.

이제 우리의 코드에서 말한 모든 것은 제가 particle_swarm_optimizer.py 라는 .py 파일 안에 있습니다.

간단히 설명해 드리겠습니다:

• Particle()은 단일 입자를 구축합니다. 무작위 위치로 시작하고, 그런 다음 위에서 말한대로 속도와 위치를 업데이트하기 위해 update_velocity() 및 update_position() 기능을 가지고 있습니다 (내가 거짓말을 하는 게 아니라는 것을 확인할 수 있습니다).
• ParticleSwarmOptimizer()는 두 가지 객체를 사용합니다: Particle() 클래스는 클래스를 구축하기 위해 사용됩니다 (입자의 기능을 추가하거나 업데이트 기능을 수정하여 알고리즘을 더 복잡하게 만들 수 있습니다). objective_function은 최소화하고자 하는 블랙 박스 함수입니다.

이제 쇼의 주인공은 물론 ParticleSwarmOptimizer()입니다. optimize()를 사용하여 최적화 프로세스를 실행할 것입니다. 결과를 출력할지 (반복별로)와 솔루션 배열을 출력할지 선택할 수 있습니다 (다시 말해, 반복별로). plot_pso_convergence()는 플로팅 단계에서 도움이 될 것입니다. animated=True로 설정하면 수렴 .GIF를 얻게 되며, 이는 전역 최솟값이 반복별로 이동하는 것을 볼 수 있음을 의미합니다 (정말 멋진 것이에요, 곧 보게 될 겁니다).

3. 실습 예제

이전에 모든 작업을 처리했으니 이제 매우 적은 라인으로 모든 것을 실행할 수 있게 되었습니다. 매우 간단한 이차 함수를 선택한다면:

이것이 저희가 생성한 .GIF입니다:

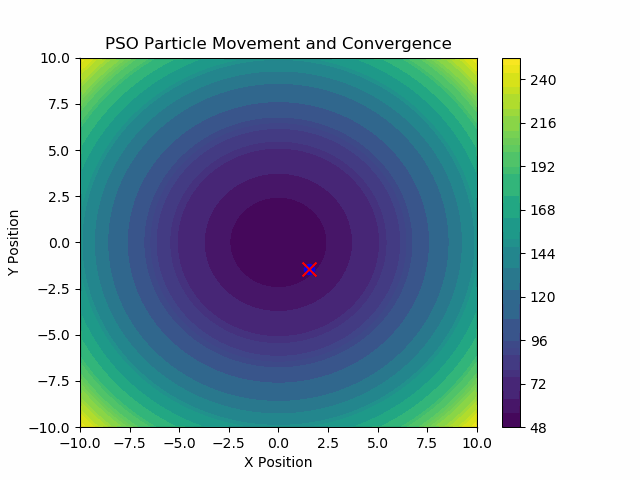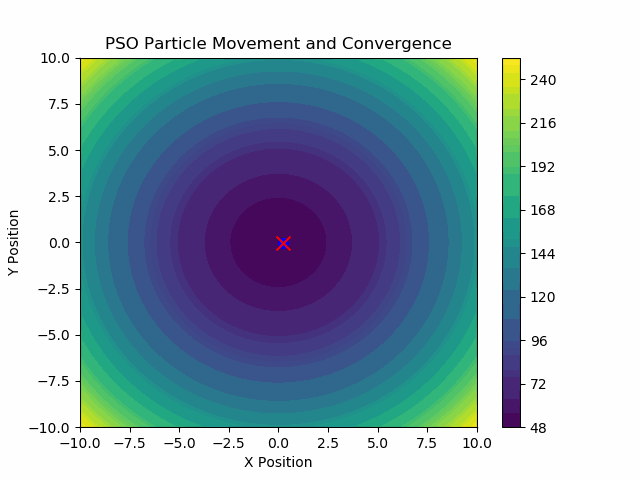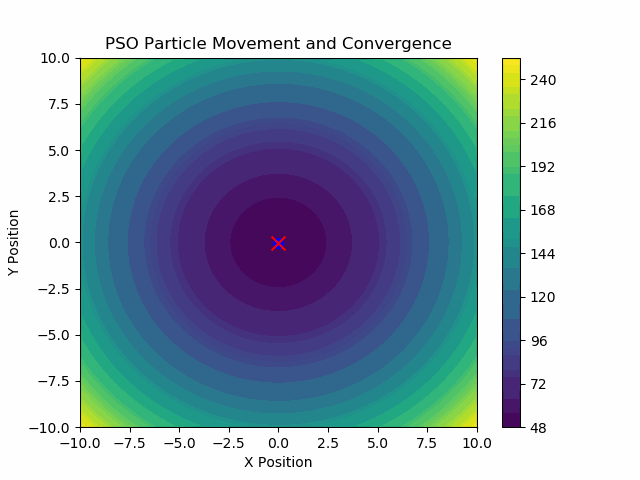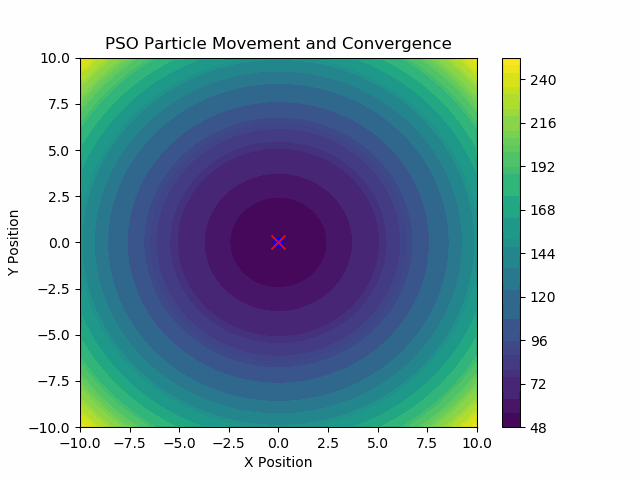
이제 PSO는 다음과 같은 꽤 복잡한 목적 함수들에서도 아주 잘 작동합니다:

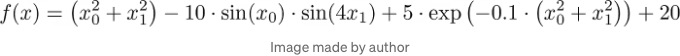
위의 코드를 실행하면 다음과 같은 결과가 나옵니다:

이것이 .GIF입니다:

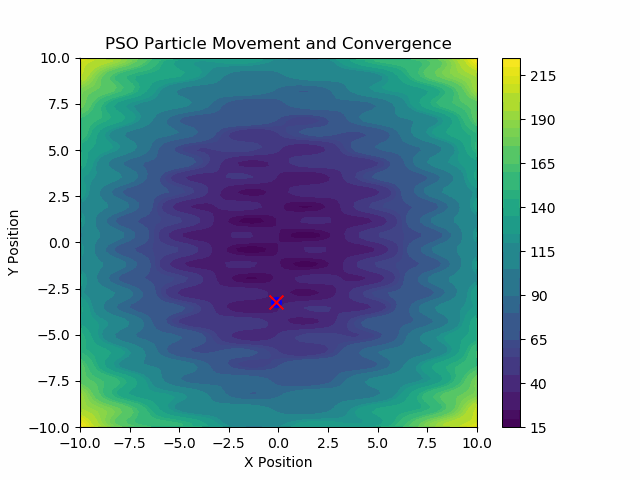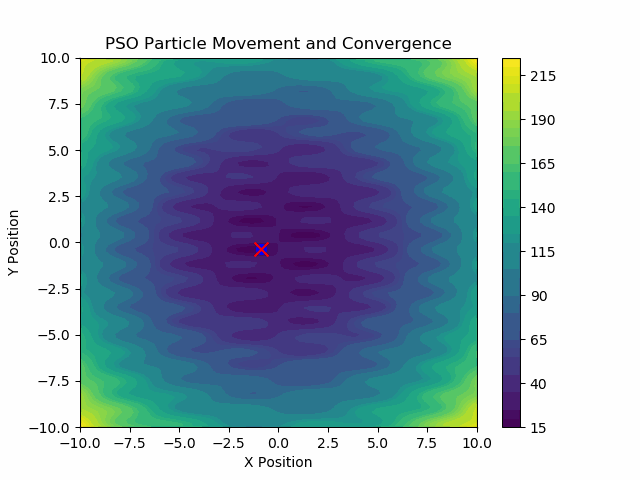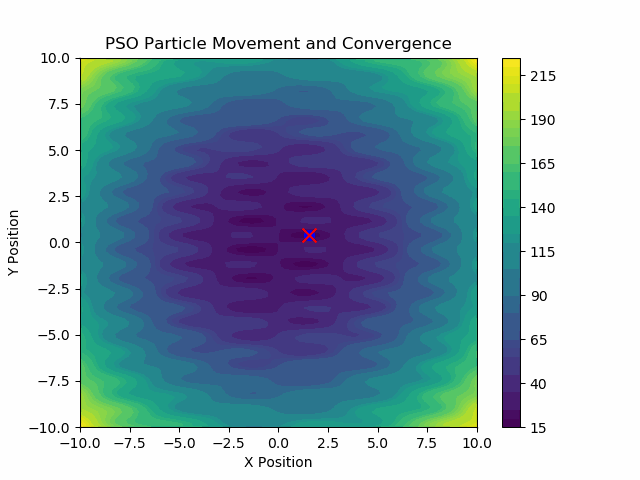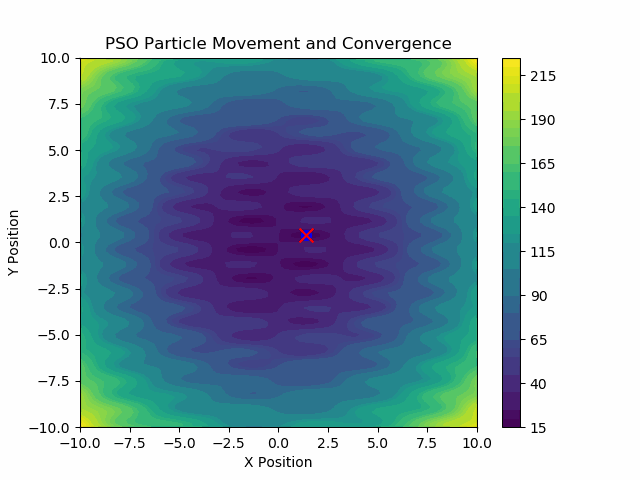
따라서 우리의 작은 PSO는 분명히 하나의 명백한 최솟값이 있는 경우에만 그 최솟값에 다다르는 것이 아니라, 더 복잡하고 여러 지역 최솟값이 있는 경우에도 글로벌(분석적으로 확인할 수는 없지만) 최솟값에 다다를 수 있음을 확인할 수 있습니다.

4. 결론

이 최적화 프로세스에서 저와 시간을 보내 주셔서 정말 감사합니다. Towards Data Science 블로그 게시물의 매개변수를 생각하면 여러분의 지식을 최대한 확장했기를 바랍니다. 🙂

본문에서는 다음과 같은 내용을 다뤘습니다:

• 여러 입자들의 정보를 동시에 분석하여 문제에 대한 작업하는 아이디어를 설명했습니다.
• "최적화" 작업을 집 값 최소화의 매우 단순한 사례로 설명했습니다.
• 일반적인 용어로 Particle Swarm Optimization (PSO)에 대해 이야기하고 흥미로운 아이디어에 대해 이야기했습니다.
• 연립 방정식의 세계로 들어가 알고리즘이 초기에 무작위 상태로 num_particles 입자를 진화시켜 전역 최솟값의 가장 적합한 추정치에 도달하는 방법을 보았습니다.
• 객체지향 프로그래밍을 사용하여 PSO를 처음부터 구현했습니다.
• 매우 간단한 2차 함수 문제와 훨씬 더 복잡한 다중 극소 문제에서 테스트를 실시했습니다. 두 경우 모두 매우 유망한 결과를 얻었습니다!

5. 나에 대해!

다시 한번 시간 내주셔서 감사합니다. 정말 감사해요 ❤

제 이름은 Piero Paialunga이고, 이 사람이에요:

이미지는 저자가 제작했습니다.

안녕하세요! 저는 시칸나티 대학 항공우주공학부의 박사 후보이자 Gen Nine의 머신 러닝 엔지니어입니다. 블로그 글과 Linkedin에서 AI 및 머신 러닝에 대해 이야기합니다. 만약 이 기사를 좋아하셨고 머신 러닝에 대해 더 알고 싶으시다면:

A. 링크드인에서 저를 팔로우해주세요. 제 이야기들을 모두 게시하고 있습니다. B. 뉴스레터를 구독해주세요. 새로운 이야기에 대한 업데이트를 제공하며, 궁금한 사항이나 수정 사항이 있을 때 텍스트로 보내주실 수 있습니다. C. 추천 멤버가 되어 "월별 최대 이야기 수" 제한 없이 읽을 수 있습니다. 그리고 수천 명의 다른 머신 러닝 및 데이터 과학 최고 작가가 제공하는 최신 기술에 대해 읽을 수 있습니다. D. 저와 함께 일하고 싶으신가요? Upwork에서 요금 및 프로젝트를 확인해주세요!

질문이 있거나 협업을 시작하고 싶으시면 이곳이나 링크드인에 메시지를 남겨주세요:

piero.paialunga@hotmail.com

Timeseries

Neural Networks